ComplexFit fits only part of fit parameters

Question

I'm trying to fit experimental complex data with model:

model = s/(1-I*t*fr)

In the model I want to find real-valued parameters s and t, while fr is free parameter. I'm looking for parameters in the range:

10^11 < fr < 3*10^12,
(Ranges for parameter values)
10^-4 < s < 10^-3 
10^-14 < t < 10^-12.

From reading related questions I've found out about Oleksandr R.'s fitting package ComplexFit which I at least tried to fit my data. From answers in other threads I've figured out how to set parameters to be real values, but the the function seems to be fitting only one parameter instead of both.

Here is my code:

model=s/(1-I*t*fr);
ComplexFit[shortdata, {model, 
{TransformedParameter[Re, s] > 0, TransformedParameter[Re, t] > 0}},
{{s, 0.00079}, {t, 0.4*10^-12}}, fr, 
"CoordinateSystem" -> "Real",
Method -> {NMinimize,
Method -> {"DifferentialEvolution",
"SearchPoints" -> 25, "ScalingFactor" -> 0.95, "CrossProbability" -> 0.05,
"PostProcess" -> {FindMinimum, Method -> "QuasiNewton"}}}]
{Re[s]->0.00079,Re[t]->1.44266*10^-13}

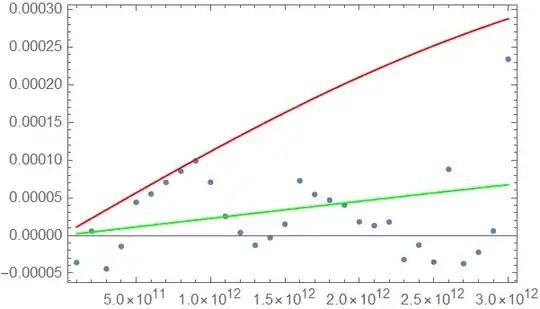
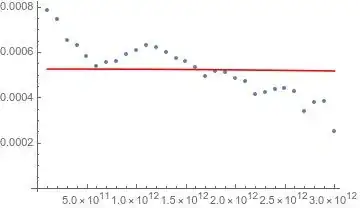
Any value of s I set into prediction ends up in fitting result unchanged, while t varies. Below you can see how "fitted" model relates to data:

Show[{
ListPlot[Re[shortdata], PlotRange->{{1*10^11,3*10^12},{0,0.0015}}, ImageSize->Large, 
PlotStyle->PointSize[Medium], PlotLegends->{"Data"}],
Plot[Re[0.00079/(1-I*1.44266*10^-13*fr)], {fr, 1*10^11,3*10^12}, PlotRange->All, 
PlotLegends->{"Model@Fit parameters"}, PlotStyle->Red]}]

It is not absolutely useless, but it's not very close. Also I've tried to use NonlinearModelFit, in the ComplexFit framework, but it is not returning fitted parameters:

ComplexFit[shortdata, {model, 
{TransformedParameter[Re, s] > 0, TransformedParameter[Re, t] > 0}},
{{s, 0.00079}, {t, 0.4*10^-12}}, fr, 
"CoordinateSystem" -> "Real",
"FitFunction" -> NonlinearModelFit]

Output:

FittedModel[0.185477 If[TransformedFit`Private`i==2,1,0] Im[1/(1-(0. +0.185477 I) fr)]
+0.185477 If[TransformedFit`Private`i==1,1,0] Re[1/(1-(0. +0.185477 I) fr)]

Could someone explain why first set of code is not fitting parameter s?

Below I attach the experimental data used for fitting:

data={{9.99898*10^10, 0.000785013 - 0.0000358699 I}, {1.9998*10^11, 
0.000743333 + 5.74186*10^-6 I}, {2.99969*10^11, 
0.000651463 - 0.0000441542 I}, {3.99959*10^11, 
0.000631073 - 0.0000144929 I}, {4.99949*10^11, 
0.00058382 + 0.0000441497 I}, {5.99939*10^11, 
0.000537251 + 0.0000552459 I}, {6.99928*10^11, 
0.000553852 + 0.0000706242 I}, {7.99918*10^11, 
0.000558788 + 0.0000855169 I}, {8.99908*10^11, 
0.000588947 + 0.0000991657 I}, {9.99898*10^11, 
0.000606958 + 0.0000708635 I}, {1.09989*10^12, 
0.000628659 + 0.0000255788 I}, {1.19988*10^12, 
0.00062069 + 3.92344*10^-6 I}, {1.29987*10^12, 
0.000601398 - 0.0000129042 I}, {1.39986*10^12, 
0.000573754 - 2.91557*10^-6 I}, {1.49985*10^12, 
0.000558206 + 0.0000151073 I}, {1.59984*10^12, 
0.000532454 + 0.0000727382 I}, {1.69983*10^12, 
0.000493984 + 0.0000545511 I}, {1.79982*10^12, 
0.000515422 + 0.0000471141 I}, {1.89981*10^12, 
0.000513342 + 0.0000405801 I}, {1.9998*10^12, 
0.000486615 + 0.0000182233 I}, {2.09979*10^12, 
0.000470626 + 0.0000132746 I}, {2.19977*10^12, 
0.000415248 + 0.0000179242 I}, {2.29976*10^12, 
0.000425405 - 0.0000319184 I}, {2.39975*10^12, 
0.00043476 - 0.0000125093 I}, {2.49974*10^12, 
0.000440412 - 0.0000352567 I}, {2.59973*10^12, 
0.000425539 + 0.0000880937 I}, {2.69972*10^12, 
0.000339714 - 0.0000373581 I}, {2.79971*10^12, 
0.000378732 - 0.0000221571 I}, {2.8997*10^12, 
0.000384204 + 6.18219*10^-6 I}, {2.99969*10^12, 
0.000250732 + 0.000234347 I}}

Answer 1

Taking some ideas from Feyre answer on this thread and simplifying task by fitting real part separately, I've modified model parameter fitting constraints to the ones specified in my question:

model=Re[s/(1 - I*t*fr)];
fit=ComplexFit[Re[data], {model, 
{10^-4 <= TransformedParameter[Re, s] <= 10^-3, 
10^-14 <= TransformedParameter[Re, t] <= 10^-12}},
{{s, 0.0004}, {t, 1*10^-12}}, fr, 
"CoordinateSystem" -> "Real",
Method -> {NMinimize,
Method -> {"DifferentialEvolution",
"SearchPoints" -> 25, "ScalingFactor" -> 0.95, "CrossProbability" -> 0.05,
"PostProcess" -> {FindMinimum, Method -> "QuasiNewton"}}}]

{Re[s]->0.000663205,Re[t]->3.17564*10^-13}

Which seems to fit much better. Take notice, that now initial parameters do not carry over to the result. To compare I've plotted original fitting line, Hans Olo suggestion and my updated fit:

Answer 2

One actually doesn't need fancy packages to fit complex data, as simple least-squares, with a small modification, will suffice. In this case we can define a $\chi^2$ as $$ \chi^2=V^\dagger V,$$ where the $\dagger$ is the conjugate transpose and the vector $V^i$ is given by $$V^i=y^i-model(x^i).$$

This can be translated to Mathematica as follows:

model[fr_, s_, t_] := s/(1 - I*t*fr)
chi2[s_, t_] := Module[{vec},vec = Table[data[[i, 2]]-model[data[[i, 1]],s,t],{i, 1, Length[data]}];Chop[Conjugate[vec].vec]]

which for example gives

In[6]:= chi2[10^-3, 10^-13]
Out[6]= 6.91052*10^-6

and the $\chi^2$ can readily be minimized:

In[7]:= fmin = FindMinimum[chi2[s, t], {s, 10^-3, 1.1 10^-3}, {t, 10^-14, 5*10^-14}]
Out[7]= {4.76068*10^-7, {s -> 0.000526932, t -> 4.35284*10^-14}}

Plotting the real and imaginary parts of the model with the new fit (green line) shows a marked improvement over ComplexFit (red line), for the real part:

Show[ListPlot[data /. {x_, y_} -> {x, Re[y]}],Plot[{Re[model[fr, s, t]] /. fmin[[2]],  Re[0.00079/(1 - I*1.44266*10^-13*fr)]}, {fr, 1*10^11, 3*10^12},PlotStyle -> {Green, Red}],PlotRange -> {{1*10^11, 3*10^12}, {0, 0.0015}}, Frame -> True]

and for the imaginary part:

Show[ListPlot[data /. {x_, y_} -> {x, Im[y]}],Plot[{Im[model[fr, s, t]] /. fmin[[2]],Im[0.00079/(1 - I*1.44266*10^-13*fr)]}, {fr, 1*10^11, 3*10^12}, PlotStyle -> {Green, Red}], PlotRange -> {{1*10^11, 3*10^12}, All},Frame -> True]

Alas, in both cases the model does not seem to capture the features of the data, thus some alternative parameterization might be more desirable.

The above code can readily be extended to include weights, e.g. in the form of errors, and correlations between the data points, in the form of a covariance matrix.

Answer 3

Fitting explicitly the real and imaginary parts.

mx[fr_, s_, t_] := s/(1 + t^2 fr^2)
my[fr_, s_, t_] := s t fr/(1 + t^2 fr^2)
frk = Transpose[data][[1]];
zk = Transpose[data][[2]];
zkr = Re[zk];
zki = Im[zk];
obj = Sum[(mx[frk[[k]], s, t] - zkr[[k]])^2 + (my[frk[[k]], s, t] - zki[[k]])^2, {k, 1, Length[zk]}];
sol = NMinimize[{obj, 10^-4 < s < 10^-3, 10^-14 < t < 10^-12.}, {s, t}]
zkre = Join[{frk}, {zkr}] // Transpose;
zkim = Join[{frk}, {zki}] // Transpose;
Show[ListPlot[zkre], Plot[(mx[fr, s, t] /. sol[[2]]), {fr, Min[frk], Max[frk]}, PlotStyle -> Red], PlotRange -> All]
Show[ListPlot[zkim], Plot[(my[fr, s, t] /. sol[[2]]), {fr, Min[frk], Max[frk]}, PlotStyle -> Red], PlotRange -> All]