Let us consider the following martingale "compensated compound Poisson process" $M_t=\sum_{k=1}^{N_t} Z_k-\lambda t E(Z)$ where $N_t$ is a Poisson process with intensity $\lambda$, $Z_k$ is iid random variable and indepent with $N_t$.
If we consider a special case on "Stochastic Calculus for Jump Processes(https://personal.ntu.edu.sg/nprivault/MA5182/stochastic-calculus-jump-processes.pdf)" P703. We have the following figure  The author get it from software R. You can see the original code from the following picture
The author get it from software R. You can see the original code from the following picture  . My problem is that how can I get the similar simulation from Mathematica?
. My problem is that how can I get the similar simulation from Mathematica?
Asked
Active
Viewed 221 times
0
Ailiy Evan
- 103
- 3
-
1Please add the Mathematica code you have tried and the problems you have encountered. – bbgodfrey Aug 02 '21 at 12:52
-
SeedRandom[1]; With[{[Lambda] = 0.6, [Mu] = 0.5, x0 = 1}, proc = ItoProcess[m'[t] = y'[t] - [Lambda] *[Mu], m[t], {m[0], x0}, y [Distributed] CompoundPoissonProcess[ 0.5, ExponentialDistribution[1]]]; rp = RandomFunction[proc, {0., 5., 0.01}]] ListLinePlot[rp] – Ailiy Evan Aug 02 '21 at 16:28
-
Here is the Mathematica code I have tried. But It doe not work. – Ailiy Evan Aug 02 '21 at 16:29
-
Maybe I should not use the ItoProcess. But I have no idea to simulate it. – Ailiy Evan Aug 02 '21 at 17:26
1 Answers
1
TransformedProcess may be helpful.
For example:
p = CompoundPoissonProcess[.5, ExponentialDistribution[1]];
tr = TransformedProcess[x[t] - Mean[p[t]], {x \[Distributed] p}, t];
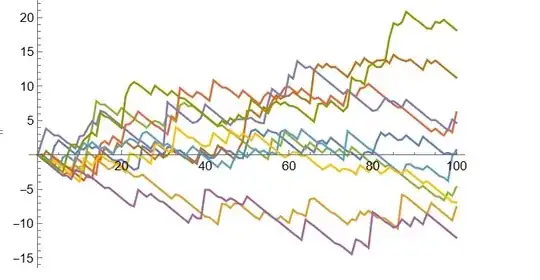
rf = RandomFunction[tr, {0, 100}, 10];
ListPlot[rf, Joined -> True]
ubpdqn
- 60,617
- 3
- 59
- 148