Why does NDSolve run into problems here?

Question

I am looking at a particle moving in a funny potential, described by the following differential equation. The solution should be just some kind of periodic trajectory, why is there a problem here?

Edit: here is the code:

k = NDSolve[{x'[t]^2 + 1/Cos[x[t]]^2 == 2, x[0] == 0}, 
  x[t], {t, 0, 4}]

Please provide your Mathematica code for this interesting problem! — Ulrich Neumann, Aug 11 '21 at 16:20
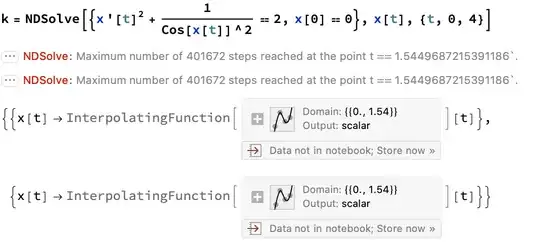
Assuming x[t] to be real your ode evaluates negative x'[t]^2 for x[t]>= Pi/4 !!! That's why NDSolve stops for x[t]==Pi/4. — Ulrich Neumann, Aug 11 '21 at 16:52
@korni1990 It evaluates to false, because 1/Cos[x[t]]^2 will get larger than 2 and the other term is squared. — Coolwater, Aug 11 '21 at 18:33
I see, thanks! But why is x[t] not simply decreasing after reaching the 'turning point' as it should? Is this not possible with NDSolve? — korni1990, Aug 11 '21 at 18:36
At the turning point, the ODE is equivalent to x'[t] == 0: The solution should be constant, not oscillatory. Check out NDSolve[{x'[t]^2 + 1/Cos[x[t]]^2 == 2, x[0] == Pi/4}, x, {t, 0, 4}, Method -> {"EquationSimplification" -> "Residual"}]. The reason it's does not become constant in Domen's answer is that numerical error prevents the solution from reaching equilibrium. That's also why your code failed, although the different methods lead to different outputs. — Michael E2, Aug 11 '21 at 23:32
@MichaelE2, is it correct to say, that the OP's DE has a singular solution $x=\pm \pi/4$, and that formally, the solution in my answer is "glued" together by two distinct nonsingular solutions? Technically, there can also be a larger constant portion of $x=\pm \pi/4$ at the turning points, and this will still be a valid solution. — Domen, Aug 12 '21 at 12:10
@Domen Yes, that’s about right. Mathematically it’s similar to https://mathematica.stackexchange.com/a/89385. The resemblance can better be seen by analyzing Coolwater’s approach. Numerically I think it’s a bit different: The two solutions for x’[t] approach each other as x[t] approaches either singular solution x[t] == ±Pi/4. One solution leads towards the singular solution and the other leads away. The step size decreases as the solution gets close to ±Pi/4, but eventually the implicit solver accidentally finds the branch leading away from the singular solution. I may answer in time. — Michael E2, Aug 12 '21 at 14:19

score 6 · Accepted Answer · answered Aug 11 '21 at 18:38

6

Your differential equation has a singularity at $x(t) = \pi/2 \approx 1.54$, and that is why the integrator has troubles approaching that point. To solve this, use:

Initial value for the first derivative

$$x(0) = 0 \implies x'(0) = \pm 1$$

Method -> {"EquationSimplification" -> "Residual"}

k = NDSolve[{x'[t]^2 + 1/Cos[x[t]]^2 == 2, x'[0] == 1
   }, x[t], {t, 0, 10}, 
  Method -> {"EquationSimplification" -> "Residual"}] 
Plot[Evaluate[x[t]] /. k, {t, 0, 10}]

Mathematica graphics

answered Aug 11 '21 at 18:38

Domen

23,608
1
27
45

Cool thanks, that does the job indeed. – korni1990 Aug 11 '21 at 19:11
Your code in "12.3.1 for Mac OS X x86 (64-bit) (June 19, 2021)" gives an error: "NDSolve::ndcf: Repeated convergence test failure at t == 7.7854479164218`; unable to continue." Are you using a different version, or did you do something not shown in the code? – Michael E2 Aug 11 '21 at 22:50
@MichaelE2 No, I run exactly the same code in 12.3.0 for Microsoft Windows (64-bit) (May 10, 2021) without errors. – Domen Aug 12 '21 at 11:47
In my case, NDSolve is probably stepping slightly below -Pi/4, but I wonder what changed (assuming it’s version-related, not OS/CPU related). – Michael E2 Aug 12 '21 at 14:23

score 2 · Answer 2 · answered Aug 12 '21 at 04:30

Your initial condition implies x[0] == 0 && x'[0] == 1.
Using the corresponding 2nd order equation works well:

eq = D[x'[t]^2 + 1/Cos[x[t]]^2 == 2, t];
sols = x[t] /. NDSolve[{eq, x[0] == 0, x'[0] == 1}, x[t], {t, 0, 5}];
Plot[sols, {t, 0, 5}, PlotRange -> All]

Why does NDSolve run into problems here?

2 Answers2