How can I draw a polygon from a set of angles?

Question

In recreational mathematics, polytans are polygons formed by edge-connecting isosceles right triangles. Order-n polytans are those constructed from n such triangles. My question is this:

Given a set of n angles and an N x N grid, how do I draw a graph using a set of angles? I am trying to find if the angles form the perimeter of a polytan (i.e., given a starting point on the plane, does progressively iterating through the angles get me back to the point of origin?). For example, given these three sets: {{270, 315, 315}, {315, 270, 315}, {315, 315, 270}}, the output would show two isosceles right triangles: {270, 315, 315} and {315, 315, 270}, and one non-polygon: {315, 270, 315}, as seen in the image below. In the image, the initial reference line is {{0,0}->{0,1} (on the y-axis), and the point of origin is {0,1}.

enter image description here

I need the constructions to be graphs so that I can check whether two polytans of the same order are identical, but just in different orientations (like the two triangles in the image). Vertex count, vertex degree, edge-connectedness, etc., would also be useful.

I'm not sure I understand you precisely. Is this what you want: Input a set of angles, judge whether it's corresponding to a polytan or not, if yes draw it out. — Silvia, May 17 '13 at 00:37
http://demonstrations.wolfram.com/OrientedTriangleAngles/ This is a demon about OrientedTriangleAngles. — HyperGroups, May 17 '13 at 01:25
@Silva: Ultimately, yes, but initially no. For now, I just want to draw everything, as I did in the image. — jnthn, May 17 '13 at 01:26
@HyperGroups: I'll take a look at the code, if I can. Thanks. EDIT: hmmm, I seems to be able to draw a 90/45/44 triangle with that demo. ;) — jnthn, May 17 '13 at 01:29
I think if you consider your edges and vertices on complex plane, it might be easier. — Silvia, May 17 '13 at 01:30

Silvia · Accepted Answer · 2013-05-17T04:50:29.457

I think you can regard each one of your edges/vertices as a complex number, so walk along the path given an angle set will be equivalent to adding the corresponding number set successively. And if the total is $0$, it means the path is closed, thus a polytan.

This is a possible implementation:

Clear[polytanPlot]
polytanPlot[angleSet_] :=
 Module[{stepVecSet},

   (* step set represented as complex numbers: *)

  stepVecSet = 
   If[IntegerQ[#/(π/2)], 1, Sqrt[2]] Exp[# I] I & /@ 
    Mod[Accumulate[angleSet - π], 2 π];

   (* closed path criterion: *)

  If[Chop[N[Total[stepVecSet]]] != 0,
   Style[Row[{Style[angleSet, 13],  " is not a valid polytan angle set!"}], 15, Red],

   (* draw the polytan: *)

   pts = Through[{Re, Im}@Accumulate[stepVecSet]]\[Transpose];
   Graphics[{FaceForm[], EdgeForm[{Thick, Blue}],
     Polygon[pts],
     Darker[Green], AbsolutePointSize[15], Point[pts]},
    Frame -> True, PlotLabel -> Style[angleSet, 13]]
   ]]

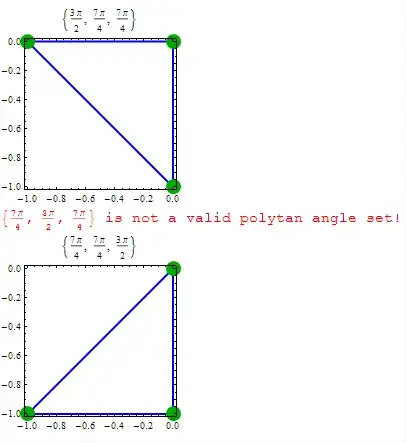
polytanPlot /@ FullSimplify[
   {{270, 315, 315}, {315, 270, 315}, {315, 315, 270}} π/180
   ] // Column

original examples

Cases[polytanPlot /@ RandomChoice[π/4 Range[7], {1000, 10}],  Graphics[__], ∞]

random examples

Edit:

For the test data set asked by OP in the comment:

testSets = Select[Tuples[{0,45,90,135,180,225,270,315}, 5], Total[#] == (5 + 2)*180 &];
Cases[polytanPlot /@ FullSimplify[testSets π/180], Graphics[__], ∞]

required

Note the interior angles at some vertices are $0$, so adjacent edges there get overlapped. Also some edges intersect each other at some non-vertex point (e.g. in the last graph above), makes it look like triangles with length $1$ hypotenuse, although they are merely self-intersected polytans.

If we want to avoid polytans with overlapped edges or with sub-polytans in it, we can test the closed path criterion on every continuous sub-set of the input angle set. This modified version might decrease the number of self-intersected result too, if not totally prevent.

Clear[polytanPlot2]
polytanPlot2[angleSet_] :=
 Module[{stepVecSet, len, nosubCircuitQ, pts},
  stepVecSet = If[IntegerQ[#/(π/2)], 1, Sqrt[2]] Exp[# I] I & /@
    Mod[Accumulate[angleSet - π], 2 π];
  len = Length[stepVecSet];
  nosubCircuitQ = True;
  Table[
   If[#, nosubCircuitQ = False; Goto["label"]] &[
    Chop[N[Total[stepVecSet[[i ;; j]]]]] == 0],
   {i, len - 1}, {j, i + 1, If[i == 1, len - 1, len]}];
  Label["label"];
  If[nosubCircuitQ && Chop[N[Total[stepVecSet]]] == 0,
   pts = Through[{Re, Im}@Accumulate[stepVecSet]]\[Transpose];
   Graphics[{FaceForm[], EdgeForm[{Thick, Blue}],
     Polygon[pts],
     Darker[Green], AbsolutePointSize[15], Point[pts]},
    Frame -> True, PlotLabel -> Style[angleSet, 13]],
   Style[Row[{Style[angleSet, 13], 
      " is not a valid polytan angle set!"}], 15, Red]
   ]]

Cases[polytanPlot2 /@ FullSimplify[testSets π/180], Graphics[__], ∞]

required 2

Self-intersected results are still found:

Cases[polytanPlot /@ RandomChoice[π/4 Range[7], {2000, 15}],  Graphics[__], ∞]

self-intersection

Edit 2:

According to J.M.'s comment, we can use an undocumented function Graphics`Mesh`SimplePolygonQ[] to achieve the purpose of avoiding both overlappings and self-intersections:

Clear[polytanPlot3]
polytanPlot3[angleSet_] :=
 Module[{stepVecSet, pts, polyg},
  stepVecSet = If[IntegerQ[#/(π/2)], 1, Sqrt[2]] Exp[# I] I & /@
    Mod[Accumulate[angleSet - π], 2 π];

  If[Chop[N[Total[stepVecSet]]] != 0,

   Style[Row[{Style[angleSet, 13], " is not a valid polytan angle set!"}], 15, Red],

   pts = Through[{Re, Im}@Accumulate[stepVecSet]]\[Transpose];
   polyg = Polygon[pts];
   If[Graphics`Mesh`SimplePolygonQ[polyg],

    Graphics[{FaceForm[], EdgeForm[{Thick, Blue}], polyg,
      Darker[Green], AbsolutePointSize[15], Point[pts]
         }, Frame -> True, PlotLabel -> Style[angleSet, 13]],

    Style[Row[{Style[angleSet, 13], " is not a simple polytan angle set!"}], 15, Red]
    ]
   ]]

Cases[polytanPlot3 /@ RandomChoice[π/4 Range[7], {2000, 15}],  Graphics[__], ∞]

final version

Wow, this is so close. Thank you so much. I will have to study this for awhile. I think "If[IntegerQ[#/(π/2)], 1, Sqrt[2]]" is causing some diagonals to be drawn incorrectly?? Test this set: Select[Tuples[{0, 45, 90, 135, 180, 225, 270, 315}, 5] , Total[#] == (5 + 2)180 &]* --all the possible angle sets for order-3 polytans. — jnthn, May 17 '13 at 02:45
@jnthn If you see some error messages, maybe using π/180 instead of the degree symbol \[Degree]. — Silvia, May 17 '13 at 02:54
@jnthn Sorry I'm not catching you.. What do you mean by "some diagonals ... drawn incorrectly"? Do you mean some edges are overlapped? — Silvia, May 17 '13 at 03:12
π/180 got rid of the Floor[] errors. ty. If you use the order-3 sets as input, you will see that the squares with the 'X' in the center have hypotenuses of length 1, rather than length $\sqrt 2$. And there is a similar problem with the "house" shape. Is that error coming from the If[] statement, do you think? — jnthn, May 17 '13 at 03:32
@jnthn Hmm.. I think they are correctly (if I understand your intention in OP correctly..) composed with length $1$ edges along axes directions and length $\sqrt{2}$ along angle bisectors of axes. — Silvia, May 17 '13 at 03:42
Maybe I didn't make this clear...the triangles need to be of equal size. I will add an image to my original post showing you the problem I see.. — jnthn, May 17 '13 at 03:46
You might be interested in the (undocumented) function Graphics`Mesh`SimplePolygonQ[] for checking self-intersections. You just need to give it a Polygon[] as an argument. — J. M.'s missing motivation, May 17 '13 at 04:33
Very very nice! After looking at the "house" shape (polygon #10 in the first EDIT section) more closely I realized it was being drawn correctly. I can now see that I will have to add an area check to weed out results that have area not equal to n times a unit triangle. Again, thanks so much Silvia. — jnthn, May 17 '13 at 16:33

How can I draw a polygon from a set of angles?

1 Answers1

Edit:

Edit 2:

Linked