EasyFourier by @xzczd is a nice package to obtain a Fourier series in closed form, e.g.
f = x^2
easyFourierTrigSeries[f, {x, -\[Pi], \[Pi]}, \[Infinity]]
However, the output cannot be manipulated symbolically, at least I don't know how to. For instance, differentiating the Fourier series is not possible like this:
D[easyFourierTrigSeries[f, {x, -\[Pi], \[Pi]}, \[Infinity]],x]
What I would like to do is something comparable to the following, where I have copied the summand manually into a regular Mathematica Sum:
BTW: How do I downscale the size of pictures in stack exchange? Is there no easier way to insert Mathematica output? How can I insert complicated Mathematica input code in 2d-mode? (Thanks for hints to these "meta" questions, too.)
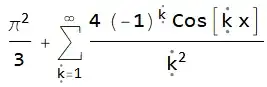


ReleaseHold?D[ReleaseHold@easyFourierTrigSeries[f, {x, -\[Pi], \[Pi]}, \[Infinity]], x]gives2 (I Log[1 + E^(-I x)] - I Log[1 + E^(I x)]). – Domen Aug 28 '21 at 15:22