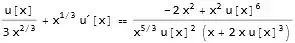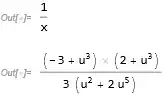Very odd results from DSolve for nonlinear ODE

Question

I am solving

$$\dfrac{dy}{dx}=\dfrac{y^6-2x^2}{xy^2\left(2y^3+x\right)}$$

In Mathematica 12.2.0.0 on Windows 10, x86, 64-bit

  DSolve[{y'[x] == (-2*x^2 + y[x]^6)/(x*y[x]^2*(x + 2*y[x]^3))}, y[x], x]

It returns a bunch of root functions like

$$\left.y(x)\to \sqrt[3]{\text{Root}\left[7290 \text{$\#$1}^2 e^{5 c_1} x^8-10125 \text{$\#$1}^3 e^{5 c_1} x^7+945 \text{$\#$1}^4 e^{5 c_1} x^6+2079 \text{$\#$1}^5 e^{5 c_1} x^5-735 \text{$\#$1}^6 e^{5 c_1} x^4-55 \text{$\#$1}^7 e^{5 c_1} x^3+75 \text{$\#$1}^8 e^{5 c_1} x^2-15 \text{$\#$1}^9 e^{5 c_1} x+\text{$\#$1}^{10} e^{5 c_1}+14580 \text{$\#$1} e^{5 c_1} x^9+x^{15}-17496 e^{5 c_1} x^{10}\&,1\right]}\right\}$$

I was not expecting this, but using step-by-step, we get something like what I was expecting

First, what are you supposed to do with all those root function outputs?

Is there some way to get the step-by-step output?

Answer 1

The solution by Wolfram alpha step by step is hand crafted. The solution by DSolve is not. It is an automated method. It looks like it did root extraction at some point since it does not see the ODE becomes separable.

You did not show the full steps Wolfram alpha used. But this is how I would do it

ClearAll[y, x, u, rhs]
ode = y'[x] == (-2*x^2 + y[x]^6)/(x*y[x]^2*(x + 2*y[x]^3));

this is isobaric of order 1/3, hence do the following substitution to make it separable

f = y -> Function[{x}, u[x]*x^(1/3)];
newOde = ode /. f

rhs = u'[x] /. First@Solve[newOde, u'[x]] /. u[x] -> u

This is separable. isobaric ODE always become separable after the substitution. The rest is now just integration. No need to use DSolve at all.

Using Leonid Shifrin code from how-can-i-separate-a-separable-function

ClearAll[getGX];
getGX[expr_, xvar_, yvar_] := 
  With[{dlogg = D[Log[expr], xvar] // FullSimplify}, 
   Exp[Integrate[dlogg, xvar]] /; FreeQ[dlogg, yvar]];
Clear[getHY];
getHY[expr_, xvar_, yvar_] := 
 FullSimplify[(#/getGX[#, xvar, yvar]) &[expr]]
fx = getGX[rhs, x, u]
fu = getHY[rhs, x, u]

Now just integrate both sides, since now the ode becomes $u'=f(x) f(u)$

solU = Integrate[1/fu, u] == Integrate[fx, x] + C[1]

substitute back to get solution of original ode

solU /. u -> y[x]/x^(1/3) // Simplify

I do not see how to tell DSolve to obtain the same hand crafted solution. Many CAS methods and algorithms do not correspond and follow the same methods we use when solving things by hand due to may reasons.

ps. for working with root objects, see Root.html and how-do-i-work-with-root-objects but since you have constant of integration in there, you will not be able to do anything with it in terms of plotting, evaluating numerical value, etc...