4

Bug fixed in 13.0.0 [CASE:4855260]

It seems that BSplineFunction always returns unevaluated without warnings, when its degree is equal to the number of control points (I'm using Mathematica 12.3.1):

n = RandomInteger[{2, 100}];
pts = RandomReal[1, {n, 2}];
f = BSplineFunction[pts, SplineDegree -> n]
f[.5]

screenshot

Why does this happen?

Note that it works as expected with degrees higher than the number of control points:

n = RandomInteger[{5, 100}];
pts = RandomReal[1, {n, 2}];
functs = Table[BSplineFunction[pts, SplineDegree -> n + i], {i, -3, 3}];
Through[functs[.5]]

out

Also notice that for degrees higher than n the outputs are equal to the output for degree n - 1:

n = RandomInteger[{5, 100}];
pts = RandomReal[1, {n, 2}];
functs = Table[BSplineFunction[pts, SplineDegree -> n + i], {i, -1, 100}];
Equal @@ Drop[Through[functs[.5]], {2}]

True

So it looks like degrees higher than n - 1 are reduced to n - 1. But why then for n it returns unevaluated? Is it a bug?

Alexey Popkov
  • 61,809
  • 7
  • 149
  • 368
  • 1
    Documentation BSplineFunction says "The dimension of the manifold represented by BSplineFunction[array] is given by ArrayDepth[array]-1. The lengths of the lists that occur at the lowest level in the array define the embedding dimension.". Perhaps that's the reason why your test only works up to SplineDegree->n-1 . – Ulrich Neumann Sep 03 '21 at 06:22
  • @UlrichNeumann But it also works with higher and lower degrees, for example SplineDegree -> n + 1 and higher! The only exception is when the degree is exactly equal to the number of points. – Alexey Popkov Sep 03 '21 at 06:35
  • Reported to support as [CASE:4855260]. – Alexey Popkov Sep 03 '21 at 07:34

1 Answers1

3

Update 2

I received a response to [CASE:4886321] (about the case of SplineClosed -> True):

Mathematica is working as designed here.

For n points, the max degree of polynomial basis one can get is n - 1.

I'm still unsure that it is correct for SplineClosed -> True, at least for an arbitrary value of the SplineKnots option, including both SplineKnots -> "Clamped" and SplineKnots -> "Unclamped" variants. There already were cases when Wolfram Technical support incorrectly rejected obvious bugs (a bright example). If you have expertise in this area, please post an answer here.

Update

The original bug is fixed in version 13.0.0. But now even for SplineClosed -> True BSplineFunction retuns for SplineDegree -> n the result identical to SplineDegree -> n - 1:

n = RandomInteger[{5, 100}];
pts = RandomReal[1, {n, 2}];
i = Random[];
BSplineFunction[pts, SplineDegree -> n, SplineClosed -> True][i] ===
 BSplineFunction[pts, SplineDegree -> n - 1, SplineClosed -> True][i]

True

In the version 12.3.1 these results were different (and both numerical):

n = RandomInteger[{5, 100}];
pts = RandomReal[1, {n, 2}];
i = Random[];
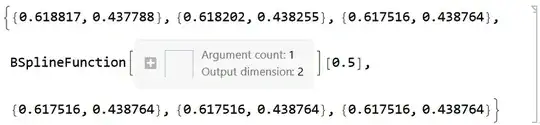
BSplineFunction[pts, SplineDegree -> n, SplineClosed -> True][i]
BSplineFunction[pts, SplineDegree -> n - 1, SplineClosed -> True][i]

{0.527505, 0.437591}

{0.52804, 0.433405}

I think that the way the original bug was fixed has introduced another bug. Reported as [CASE:4886321].

Original answer

I received a response from the support ([CASE:4855260]):

Thank you for taking the time to send your report.

I have forwarded an issue report to our developers in BSplineFunction with the information you provided, and added your contact information to the report so that you can be notified when it is resolved.

We are always interested in improving Mathematica, and I want to thank you once again for bringing this issue to our attention. If you run into any other problems with any of our products or have any additional questions, please do not hesitate to contact us.

I consider this as a confirmation that I faced a bug.

Another interesting observation is that with the option SplineClosed -> True BSplineFunction retuns numerical result for SplineDegree -> n (where n is the number of control points), but for higher values of SplineDegree it returns results equal to the output for SplineDegree -> n - 1, not SplineDegree -> n:

n = RandomInteger[{5, 100}];
pts = RandomReal[1, {n, 2}];
functs = Table[
   BSplineFunction[pts, SplineDegree -> n + i, SplineClosed -> True], {i, -1, 100}];
Equal @@ Drop[Through[functs[RandomReal[]]], {2}]
Equal @@ Through[functs[RandomReal[]]]

True

False

I consider this as another, closely related bug.

Alexey Popkov
  • 61,809
  • 7
  • 149
  • 368