Plotting equation with some unknown parameters

Question

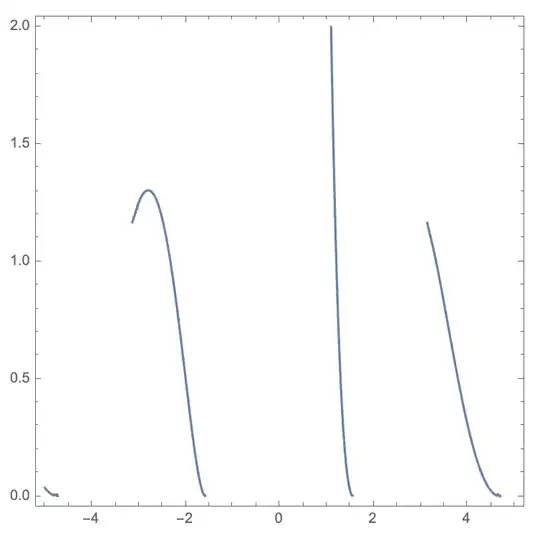
I am new to the Mathematica and I have a question about the plotting. I am trying to plot the transcendental equation

$$\tan{(z)}=\sqrt{\frac{1}{2m_0}\left (\frac{z_0}{z}\right)^2-1} $$

where the parameter $z_0=4.8$. I am just wondering can I keep the parameter $\frac{1}{2m_0}$ without specifying an exact value to it? I have searched some similar questions but still don't figure this out. Could anyone give some suggestions? Thanks!

How could the function be plotted if $m_0$ have no numerical value? You can use Manipulate to give it different values and see how the plot changes. — Nasser, Sep 08 '21 at 00:23
Solving a transcendental trygonometric equation should involve a careful analysis of the problem. Then solutions can demonstrate their geometric sense, see e.g. Solve symbolically a transcendental trigonometric equation and plot its solutions. — Artes, Sep 08 '21 at 00:56
Ummm.... how would you plot $y = a x$ for an unspecified $a$? (Of course, $a$ could be negative.) If you can solve that, well, you've solved your posted problem. — David G. Stork, Sep 08 '21 at 03:57
@Artes Oh, that help a lot! Thanks so much! The link is really good at illustrating the general idea of how to deal with this types problem...although I hope there are some better approaches. — user81752, Sep 08 '21 at 04:13

thorimur · Answer 1 · 2021-09-08T01:15:56.160

In this particular case, you can view the solution set in the $z,m_0$ plane (i.e. allowing $m_0$ to vary) with ContourPlot:

z0 = 4.8;
ContourPlot[
 Tan[z] == Sqrt[(1/(2 m0)) (z0/z)^2 - 1], {z, -5, 5}, {m0, 0, 2}, 
 PlotPoints -> 50]

(PlotPoints -> 50 just makes the resolution a bit better.)

Note: as @Artes mentions in a comment on the original question, these sorts of equations are difficult to handle. As such, the above plot might not reveal the full solution set. However, by plotting both sides of the equation in 3D and viewing the result from directly above to see where the intersections lie, it does seem we've got them all in this range.

Plot3D[{Tan[z], Sqrt[(1/(2 m0)) (z0/z)^2 - 1]}, {z, -5, 5}, {m0, 0, 2},
 PlotPoints -> 50, ViewPoint -> {0, 0, Infinity}, 
 ViewAngle -> All, Ticks -> False, AxesLabel -> Automatic, 
 PlotRange -> {-100, 100}]

Plotting equation with some unknown parameters

1 Answers1