I have a matrix with thousands of rows and want the submatrix comprising the rows of the original matrix that have, e.g. a negative element in column 3. How to do that?
Asked
Active
Viewed 2,636 times
2 Answers
7
I think this question is reasonably a duplicate of: How to find rows that have maximum value? (or several similar questions) and I will delete this answer if it is closed as such. Nevertheless, again for reference:
SeedRandom[1];
a = RandomInteger[{-3, 5}, {20, 5}]
Pick[a, Negative @ a[[All, 3]]]
{{-2, 1, -3, 4, -3}, {-2, 0, -1, -2, 3}, {1, 0, -3, -2, 0}, {2, 0, -3, 0, -1}, {0, 2, -2, 2, -1}, {0, -2, -3, 1, 1}, {-2, 2, -1, 4, 5}, {0, -1, -2, -2, 3}, {2, 3, -3, 4, -2}, {0, -2, -1, 2, 5}, {1, 4, -3, 4, 4}}
Faster in versions 8+ should be to use UnitStep, due to packed array optimizations:
Pick[a, UnitStep @ a[[All, 3]], 0]
In version 7 optimal speed may be had with:
a[[SparseArray[BitXor[UnitStep @ a[[All, 3]], 1]]["AdjacencyLists"]]]
Timings compared to other methods proposed, in version 7:
a = RandomInteger[{-3, 5}, {1500000, 5}];
Pick[a, Negative @ a[[All, 3]]] // Timing // First
a[[SparseArray[BitXor[UnitStep @ a[[All, 3]], 1]]["AdjacencyLists"]]] // Timing // First
(col3 = a[[All, 3]]; rowsToGet = Flatten[Position[col3, _?((# < 0) &)]]; a[[rowsToGet]]) //
Timing // First
Select[a, #[[3]] < 0 &] // Timing // First
0.234
0.031
0.905
1.17
4
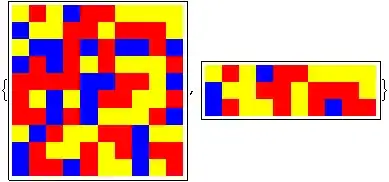
m = RandomInteger[{-1, 1}, {10, 10}];
m1 = Select[m, #[[3]] < 0 &];
Show it:
ArrayPlot[#, ColorRules -> {1 -> Red, 0 -> Blue, -1 -> Yellow, _ -> Gray}] & /@ {m, m1}
Dr. belisarius
- 115,881
- 13
- 203
- 453
Pickpicks a second almost on my i7 (+ Win7 and Mma 9). Can I tweak my system any towards the performance of yours? Another slower method, by a factor of 3.5 with my timing, is to:Scanwith levelspec{-2}andSowrows with negative third element. – BoLe May 20 '13 at 14:07Picksince version 7 but I thought they would make things faster rather than slower. – Mr.Wizard May 20 '13 at 14:50Pick[a, UnitStep @ a[[All, 3]], 0]to be best on v9. – Mr.Wizard May 20 '13 at 14:58{0.952, 0.0780, 1.84, 2.04}which make approximately same ratios as yours, somewhere 10 : 1 : 25 : 30. P.S.PickwithUnitStepis the fastest here with 0.047. – BoLe May 20 '13 at 17:51Pick[a, UnitStep @ a[[All, 3]], 0]and tell me how it performs. Thanks. – Mr.Wizard May 21 '13 at 05:35Pick[..., 0]- I just can't get it right tonight. I'm going to do something else. – Mr.Wizard May 21 '13 at 08:23