ImplicitRegion fails on apparently simple case

Question

Consider the shaded region bounded by $\sin x$, $\cos x$, and $\tan x$:

We can define this as an ImplicitRegion by:

\[ScriptCapitalR] = 
 ImplicitRegion[(0 < x < 1) \[And] (y < Cos[x]) \[And] 
     (y < Tan[x]) \[And] (y > Sin[x]),
  {x, y}]

However, RegionPlot[\[ScriptCapitalR]] fails to yield a figure after 15 minutes (v 11.3, MacOS).

However if I'm "smart" and put the bounds as $0<x< \pi/4$ I do get a plot.

Moreover, its area,

RegionMeasure[\[ScriptCapitalR]]

does not give an analytic solution (even after RootReduce, Simplify, etc.) even though an analytic form exists.

(One can get a numerical value through N@RegionMeasure[\[ScriptCapitalR]], but I seek the analytic solution.)

I've tried various forms based on RegionIntersection[] and such, without success.

Of course I can use traditional calculus through Integrate and finding intersection points, but I'd like to compute the area more directly.

How can I 1) plot the region and (more importantly) 2) compute the analytic area?

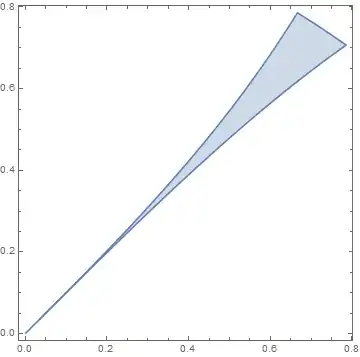
for (1) try RegionPlot[DiscretizeRegion@\[ScriptCapitalR]]? — kglr, Sep 15 '21 at 00:33
and for (2) FullSimplify[ToRadicals@RegionMeasure@\[ScriptCapitalR]] gives 1/2 (-1 + 2 Sqrt[2] - Sqrt[5] + ArcCsch[2]) (version 11.3 windows) — kglr, Sep 15 '21 at 00:37
Yep. (1) AND (2) work. Post and I'll accept. Thanks (again). — David G. Stork, Sep 15 '21 at 00:37
How is that region finite? given that the region as described repeats itself in every interval {2 n Pi, (2 n+1/4) Pi} for all n Integer? Also, why does Mathematica considers only the region for n=0? — rhermans, Sep 15 '21 at 09:17

kglr · Accepted Answer · 2021-09-15T03:37:31.160

11

1. Process ℛ with DiscretizeRegion before feeding it to RegionPlot:

ℛ = ImplicitRegion[(0 < x < 1) ∧ (y < Cos[x]) ∧ (y < Tan[x]) ∧ (y > Sin[x]), {x, y}]
RegionPlot[DiscretizeRegion @ ℛ]

2. A composition of FullSimplify and RegionMeasure gives an exact result:

FullSimplify @ RegionMeasure @ ℛ

  1/2 (-1 + 2 Sqrt[2] - Sqrt[5] + ArcCsch[2])

edited Sep 15 '21 at 03:37

answered Sep 15 '21 at 00:42

kglr

1 Answers1