I am currently working with the following integrals
\begin{equation} \int_{0}^{\infty} dk\thinspace \frac{k^{3}e^{-2kd}}{\omega^{2}+k^{4}} = \frac{1}{\omega^{2}d^{4}}\int_{0}^{\infty}d\epsilon\thinspace\frac{\epsilon^{3}e^{-2\epsilon}}{1+\frac{\epsilon^{4}}{\omega^{2}d^{4}}} \end{equation} which can be verified by the use of $\epsilon = k d$.
The problem is: depending on which side of the above equation I use, I obtain different results for its value as a function of $d$.
Here is how I define the integrals
SEND[\[Omega]_, d_] := NIntegrate[k*((k^2*Exp[-2*k*d])/((k^2)^2 + \[Omega]^2)), {k,0,Infinity}, AccuracyGoal -> 20, PrecisionGoal -> 20, MaxRecursion -> 20, WorkingPrecision -> 50]
SEdimN[[Omega], d] := (1/([Omega]^2d^4))NIntegrate[([Epsilon]^3Exp[-2[Epsilon]])/(1 + (1/([Omega]^2d^4))[Epsilon]^4), {[Epsilon], 0, Infinity},AccuracyGoal -> 20, PrecisionGoal -> 20,MaxRecursion -> 20, WorkingPrecision -> 50]
and here is how I plot them
LogLogPlot[{SEND[1, z], SEdimN[1, z]}, {z, 10^-10, 10^5}, LabelStyle -> Black, PlotLegends -> "Expressions", PlotRange -> {10^-6, 10^3}, PlotPoints -> 1000,WorkingPrecision -> 50]
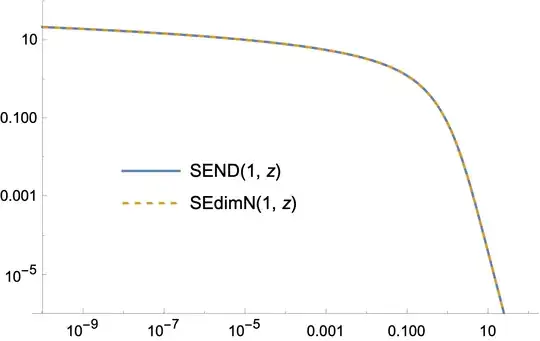
The result I obtain is something like
from where we can clearly see that for most of the range both integrals yield the same value. So my question is: Whey they are yielding different results? How do I know which one is the correct one!?


Integrate[(k^3 Exp[-2 d k])/(\[Omega]^2 + k^4) , {k, 0, \[Infinity]}, Assumptions -> d > 0 && \[Omega] > 0]. The shape of the blue curve suggests that the numerical integral is calculated with insufficient accuracy. For related issues see e.g. Numerical underflow for a scaled error function. – Artes Sep 28 '21 at 02:41