How to minimize a function involving NIntegrate?

Question

I have three datasets as follow:

d1 = {7.813540819717949`, 6.529568930239602`, 8.109143155429088`, 7.689731068450451`, 8.74120436001789`, 7.4987912906550225`, 7.615218703959835`, 8.247993113806512`, 7.2855561696238285`, 7.166026422873959`, 7.378283448111686`, 7.3970482801481445`, 7.021646802522941`, 7.1487021619286235`, 7.209809605280611`, 7.872181282365198`, 7.984087026932971`, 7.264607460785361`, 7.491235907642249`, 6.986130172036584`, 8.132032453432691`, 6.738507551311768`, 7.634485996132314`, 7.786727105539017`, 6.747498220290592`, 5.652606213674484`, 6.7145418893159245`, 7.3870764772231245`, 8.14556152457044`, 7.081683553610293`, 7.878354128765276`, 7.502128544096253`, 7.445033772765536`, 8.112365581746175`, 6.964895579434653`, 7.98895773278444`, 7.097718201996728`, 6.6447632395708816`, 7.014871229850273`, 7.596255451339725`, 7.327487147907844`, 7.626051696868463`, 7.973711939912565`, 7.497221611664195`, 7.6858101713490985`, 8.629983423881175`, 6.599398955562014`, 6.833800440038957`, 7.171926480447397`, 5.789311864786593`, 7.089675372368081`, 6.1631268127766665`, 7.639965587796188`, 7.086047166284019`, 5.406270852788866`, 6.93340616203404`, 5.807420811406816`, 6.419517442993749`, 7.414925539201528`, 7.33535213385308`, 8.263651842593319`, 6.164116766463783`, 6.947143869593553`, 6.9901653234057335`};
d2 = {3.5113704043630944, 7.608006873863145, 7.277906729276423, 8.103217766965727, 7.250931121957523, 7.8289541079690075, 6.974346234874238, 8.270349382459646, 8.10910442305307, 6.9048101280375365, 7.325825456049268, 7.73757379706066, 6.765535372291408, 6.785935805992911, 6.688548887697433, 8.459691239773468, 8.186443329842977, 6.460124310707724, 5.331370159943533, 7.509021973926822, 5.895785915422184, 7.155632848713018, 6.297014977893012, 7.024257130369493, 6.7061658261632875, 6.076510324090876, 6.619713727473183, 6.806885656438763, 6.29566021880475, 6.379851689698886, 5.886155198942714, 6.711177147084791, 6.0644975554789955, 6.476320208302014, 5.555972713843852, 5.445658305743026, 4.106563198219526, 9.662304286781078, 7.245526688643017, 7.729224257804472, 7.348730647320301, 6.811708787441987, 6.453437984409927, 6.251602287446226, 6.222552426881395, 6.325257487433763, 6.561448036981885, 6.992186187552647, 6.581755244192236, 6.35555449505844, 6.356911340563265, 5.993472986445495, 6.8937984018722185, 6.475209760379862, 5.709341745086517, 5.993789526904261, 5.81235159806516, 5.929503391669893, 6.692420198312638, 6.897925343017829, 7.935826808183915, 5.21638101511404, 6.0629537994613605, 5.011619213604298, 5.329736171185173, 5.581381723984043, 5.386724423467079, 6.8984666598061235, 6.624173458096634, 5.9758576034447595, 6.262093086610586, 6.191574403265945, 6.345257463708366, 6.691754218111958};
d3 = {11.3197, 10.9668, 10.6479, 11.6099, 10.2554, 11.3928, 11.1466, 8.62521, 9.39976, 8.52043, 9.68226, 9.16244, 9.56907, 9.6331, 10.0117, 11.9325, 11.0703, 10.2413, 10.1749, 11.377, 9.48853, 9.27371, 8.69103, 9.91404, 10.1807, 8.29698, 9.88819, 9.10128, 11.2514, 8.5246, 9.90356, 9.61888, 9.94975, 10.562, 10.3259, 10.5507, 10.3181, 10.4145, 10.6412, 9.67268, 10.5768};

Now, I need to calculate the entropy of each of the above data from their corresponding histograms; however, the bin widths of histograms are not known. I should determine the bin widths in such a way that the function $g$, defined below, to be minimized.

Thus, first, we write for the entropies as:

e1[y_] := NIntegrate[With[{f = PDF[HistogramDistribution[d1, {y}], x]}, If[f > 0, -f Log[f], 0]], {x, -\[Infinity], \[Infinity]}]
e2[z_] := NIntegrate[With[{f = PDF[HistogramDistribution[d2, {z}], x]}, If[f > 0, -f Log[f], 0]], {x, -[Infinity], [Infinity]}]
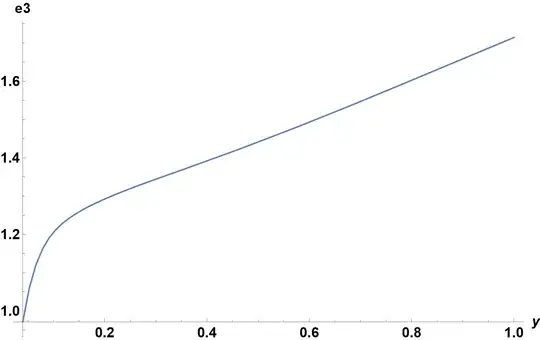
e3[w_] := NIntegrate[With[{f = PDF[HistogramDistribution[d3, {w}], x]}, If[f > 0, -f Log[f], 0]], {x, -[Infinity], [Infinity]}]

where $y$, $z$, and $w$ are the bin widths of histograms, and the entropy is defined as usual.

The bin widths should be chosen in such a way that the following function to be minimized:

g[x_, y_, z_, w_] := (0.40) Log[(0.40)/((E^(-x (e1[y])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + E^(-x (e3[w]))))]
+ (0.38) Log[(0.38)/((E^(-x (e2[z])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + E^(-x (e3[w]))))]
+ (0.22) Log[(0.22)/((E^(-x (e3[w])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + E^(-x (e3[w]))))]

so:

FindMinimum[{g[x, y, z, w], x > 0 && y > 0 && z > 0 && w > 0}, {x, y, z, w}]

At this stage, Mathematica returns errors. I think, NIntegrate cannot be defined in terms of variables. Any help is appreciated.

Answer 1

You might consider a single function for calculating the entropy values:

e[y_?NumericQ, d_] := Module[{skd, dmin, dmax, g},
  skd = SmoothKernelDistribution[d, y];
  {dmin, dmax} = MinMax[d] + 3.9 y {-1, 1};
  g = PDF[skd, a][[1, 1, 1]];
  NIntegrate[-g Log[g], {a, dmin, dmax}]]

Rather than integrating from $-\infty$ to $\infty$, I've used 3.9 times the bandwidth above and below the maximum and minimum values in the dataset. A multiplier larger than 4 will result in a zero value for the pdf and cause issues.

Also the function to be minimized can probably be simplified. If I did the simplification correctly, I get the following:

f[x_?NumericQ, y_?NumericQ, z_?NumericQ, w_?NumericQ] :=
 -1.0673063239076608 + 0.4 e[y, d1] x + 0.38 e[z, d2] x + 
  0.22 e[w, d3] x + Log[E^(-e[y, d1] x) + E^(-e[z, d2] x) + E^(-e[w, d3] x)]

Minimizing the function took about 21 minutes on my 5-year-old PC:

AbsoluteTiming[sol = FindMinimum[{f[x, y, z, w], x > 0 && y > 0 && z > 0 && w > 0}, {x, y, z, w}]]
(* {1265.76, {1.24345*10^-14, {x -> 3.92559, y -> 1.66405, z -> 1.54815, w -> 1.89182}}} *)

I don't know if a value of 1.24345*10^-14 for $f$ makes any sense or not. Different starting values (which are all 1 in this case) might result in a different set of estimated parameters.

Addition 1

Why integrate from Min[d1] - 3.9 y to Max[d1] + 3.9 y rather than $-\infty$ to $\infty$ or Min[d1] to Max[d1]?

SmoothKernelDistribution (with a Gaussian kernel) produces a pdf that has positive values from Min[d1] - 5 y to Min[d1] - 5 y and zero elsewhere:

y = 1.66405;
PDF[SmoothKernelDistribution[d1, y], x]

Min[d1] - 5*y <= x <= Max[d1] + 5*y
(* -4.59373 <= x <= 18.7412 *)

But suppose one integrated the PDF from Min[d1] to Max[d1] compared to Min[d1] - 3.9 y, Max[d1] + 3.9 y:

y = 1.66405;
NIntegrate[PDF[SmoothKernelDistribution[d1, y], x], {x, Min[d1], Max[d1]}]
(* 0.642989 *)
NIntegrate[PDF[SmoothKernelDistribution[d1, y], x], {x, Min[d1] - 3.9 y, 
  Max[d1] + 3.9 y}]
(* 0.999994 *)

Using just the min and max did not capture enough of the probability.

So why use 3.9 rather than 5 as the multiplier? For your transformation of the entropy I got underflow errors when using 5 and even when using 4. Using 3.9 seemed to capture most of the probability (i.e., integrating close to 1) and didn't produce errors.

Additional 2

Stability of the results.

Using different starting values very close to the previous results resulted in an even smaller minimum for $f$ and very different parameter values:

AbsoluteTiming[sol = FindMinimum[{f[x, y, z, w], 
    x > 0 && y > 0 && z > 0 && w > 0}, {{x, 4}, {y, 1.7}, {z, 1.5}, {w, 1.9}}]]
{888.965, {0., {x -> 4.5959, y -> 2.25562, z -> 2.18019, w -> 2.52917}}}

There appears to be some numeric stability issues. You probably need to Rationalize the constants (i.e., 0.4 -> 4/10, 0.38 -> 38/100, 0.22 -> 22/100, etc.) and raise the WorkingPrecision in FindMinimum.

Answer 2

Here is a different approach that may raise some issues with the Question itself. As I noted in comments above, the functions listed in the question are quite noisy, and FindMinimum does not converge in any reasonable amount of time. Consequently, as suggested by the OP in a comment above, JimB in his answer used an alternative function,

e[y_?NumericQ, d_] := 
    Module[{skd, dmin, dmax, g}, skd = SmoothKernelDistribution[d, y];
    {dmin, dmax} = MinMax[d] + 3.9 y {-1, 1};
    g = PDF[skd, a][[1, 1, 1]];
    NIntegrate[-g Log[g], {a, dmin, dmax}]]

Plotting this function for the three data sets in the question yields

Plot[e[y, d1], {y, .04, 1}, MaxRecursion -> 3, PlotPoints -> 10, 
    PlotRange -> All, AxesLabel -> {y, "e1"}, ImageSize -> Large, 
    LabelStyle -> {15, Bold, Black}]

Plot[e[y, d2], {y, .12, 1}, MaxRecursion -> 3, PlotPoints -> 10, 
    PlotRange -> All, AxesLabel -> {y, "e2"}, ImageSize -> Large, 
    LabelStyle -> {15, Bold, Black}]

Plot[e[y, d3], {y, .04, 1}, MaxRecursion -> 3, PlotPoints -> 10, 
    PlotRange -> All, AxesLabel -> {y, "e3"}, ImageSize -> Large, 
    LabelStyle -> {15, Bold, Black}]

Note that these plots cannot be extended to smaller values of y, because e becomes complex there. Note, also, that these plots are somewhat different from those obtained from {e1, e2, e3} in the question. They are, however, smooth.

Turn now to the quantity to be minimized. As JimB points out, it can be simplified somewhat.

Expand[FunctionExpand[(0.40) Log[(0.40)/((E^(-x (e1[
           y])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + 
       E^(-x (e3[w]))))] + (0.38) Log[(0.38)/((E^(-x (e2[
           z])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + 
       E^(-x (e3[w]))))] + (0.22) Log[(0.22)/((E^(-x (e3[
           w])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + 
       E^(-x (e3[w]))))]] /. Log[z1_ z2_] -> Log[z1] + Log[z2]]
(* -1.06731 + 0.4 Log[E^(x e1[y])] + 0.38 Log[E^(x e2[z])] + 0.22 Log[E^(x e3[w])]
    + 1. Log[E^(-x e1[y]) + E^(-x e2[z]) + E^(-x e3[w])] *)

Suppose, now, we make the substitution,

% /. {x e1[y] -> h1, x e2[z] -> h2, x e3[w] -> h3}
(* -1.06731 + 0.4 Log[E^h1] + 0.38 Log[E^h2] + 0.22 Log[E^h3] + 
   1. Log[E^-h1 + E^-h2 + E^-h3] *)

So, there are only three quantities to be varied in the minimization process. This explains in part the multiple solutions obtained by JimB. However, to perform the minimization, lower bounds must be put on {h1, h2, h3}. If we assume, arbitrarily, that x = 1, then we have from the plots above,

s = NMinimize[{%, h1 > .8, h2 > 1.3, h3 > 1}, {h1, h2, h3}]
(* {3.63403*10^-7, {h1 -> 1.2487, h2 -> 1.3, h3 -> 1.84653}} *)

obtained in a few seconds. Next, find

FindRoot[e[y, d1] - h1 /. s[[2]], {y, .4}]
(* {y -> 0.506467} *)
FindRoot[e[y, d2] - h2 /. s[[2]], {y, .127, .2}]
(* {y -> 0.161228} *)
FindRoot[e[y, d3] - h3 /. s[[2]], {y, 1.2}]
(* {y -> 1.24325} *)

Different choices for x yields different results for the arguments of e. On this basis, it would appear that the solution space {x, y, z, w} is not a point but a one-dimensional space. In fact, it is a two-dimensional space, as can be seen from

ListLinePlot3D[Table[Join[{n}, 
    ArgMin[{f /. h1 -> n, h2 > 0, h3 > 0}, {h2, h3}]], {n, 0, 1, .01}],
    BoxRatios -> {1, 1, 1}, PlotRange -> {{0, 1}, {0, 1}, {1/2, 3/2}}, 
    AxesLabel -> {h1, h2, h3}, ImageSize -> Large, LabelStyle -> {15, Bold, Black}]

and f = 0 to within 10^-6 along the curve.

Addendum - Symbolic Minimization of f

Interestingly, rationalizing f and modifying the definitions of h2 and h3 (i.e., {x e2[z] -> h1 + h2, x e3[w] -> h1 + h3}) eliminates h1.

Expand[FunctionExpand[
    (40/100) Log[(40/100)/((E^(-x (e1[y])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + 
       E^(-x (e3[w]))))] + 
    (38/100) Log[(38/100)/((E^(-x (e2[z])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + 
       E^(-x (e3[w]))))] + 
    (22/100) Log[(22/100)/((E^(-x (e3[w])))/(E^(-x (e1[y])) + E^(-x (e2[z])) + 
       E^(-x (e3[w]))))]] /. Log[z1_ z2_] -> Log[z1] + Log[z2]];
% /. {x e1[y] -> h1, x e2[z] -> h1 + h2, x e3[w] -> h1 + h3};
f = Simplify[% /. Log[Exp[z1_ + z2_]] -> Log[Exp[z1]] + Log[Exp[z2]] /. 
    Log[z1_ + z2_ + z3_] -> Log[z1] + Log[1 + z2/z1 + z3/z1], h1 >= 0]
(* 1/50 (-20 Log[5/2] - 19 Log[50/19] - 11 Log[50/11] + 19 Log[E^h2] + 
   11 Log[E^h3] + 50 Log[1 + E^-h2 + E^-h3]) *)

which minimizes to an exact solution.

FullSimplify[Minimize[{f, h2 > 0, h3 > 0}, {h2, h3}]]
(* {0, {h2 -> Log[20/19], h3 -> Log[20/11]}} *)

That h1 does not enter into this result reinforces the observation above that the original problem has a two-dimensional space of solutions. Specific values for {y, z, w} now are obtained numerically from

x e1[y] == h1
x e2[z] == h1 + Log[20/19]
x e3[w] == h1 + Log[20/11]

with positive x and h1 chosen at will.