Visualizing distribution of 3 balls in 3 cells

Question

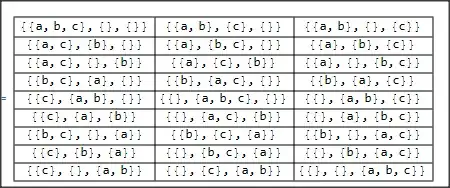
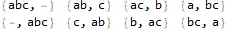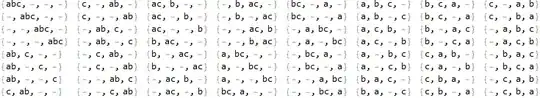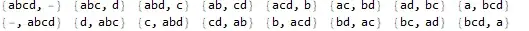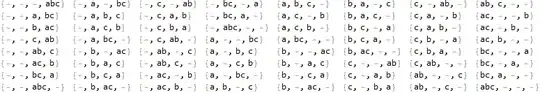I want to generate the following Table which shows the distribution of 3 balls in 3 cells. But so far I have had no luck using Permutations, Tuples, or even IntegerPartitions.

Output can be in the following form for each item in the table: {{a,b,c},{},{}} for {abc|-|-} and {{},{a,b},{c}} for {-|ab|c}

Edit: Solution based on Daniel Huber's accepted solution. Do let me know if I can simplify this further. It is a simple Mapper function that maps each tuple whose index corresponds to the ball letter (a,b, or c) and the element itself corresponds to the cell in which the ball lies (eg. tuple {1,2,2} maps to{{a},{b,c},{}}). Then we simply find all such tuples and translate them. All such tuples are Tuples[{1,2,3},3].

Mapper[i_List] := Module[{t = {{}, {}, {}}},
   Map[AppendTo[t[[i[[#]]]], {a, b, c}[[#]]] &, Range[3]]; t];
Multicolumn[Map[Mapper, Tuples[{1, 2, 3}, 3]], 3]

Output:

{{a,b,c},{},{}} {{b,c},{a},{}}  {{b,c},{},{a}}
{{a,b},{c},{}}  {{b},{a,c},{}}  {{b},{c},{a}}
{{a,b},{},{c}}  {{b},{a},{c}}   {{b},{},{a,c}}
{{a,c},{b},{}}  {{c},{a,b},{}}  {{c},{b},{a}}
{{a},{b,c},{}}  {{},{a,b,c},{}} {{},{b,c},{a}}
{{a},{b},{c}}   {{},{a,b},{c}}  {{},{b},{a,c}}
{{a,c},{},{b}}  {{c},{a},{b}}   {{c},{},{a,b}}
{{a},{c},{b}}   {{},{a,c},{b}}  {{},{c},{a,b}}
{{a},{},{b,c}}  {{},{a},{b,c}}  {{},{},{a,b,c}}

Welcome to Mathematica.SE! I hope you will become a regular contributor. To get started, 1) take the introductory [tour] now, 2) when you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge, 3) remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign, and 4) give help too, by answering questions in your areas of expertise. — bbgodfrey, Oct 14 '21 at 10:51
Similar question (but balls are not uniquely identified): https://mathematica.stackexchange.com/questions/209618/stars-and-bars-representation. — JimB, Oct 14 '21 at 17:21

kglr · Answer 1 · 2021-10-14T16:08:09.120

We can use the function partition from this answer by Mr.Wizard to get all partitions of the input list:

partition[{x_}] := {{{x}}}
partition[{r__, x_}] := 
 Join @@ (ReplaceList[#, {{b___, {S__}, a___} :> {b, {S, x}, 
         a}, {S__} :> {S, {x}}}] & /@ partition[{r}])

For each partition, use PadRight to add {} to get the desired number of bins and take Permutations:

ClearAll[binLists]
binLists[l_List, nbins_Integer] := 
 Module[{p = Join @@ (Permutations[PadRight[#, nbins, {{}}]] & /@ partition[l])}, 
  If[nbins >= Length@l, p, Select[Sort[l] == Union @@ # &]@p]]
binLists[l_List] := binLists[l, Length@l]
binLists[{a, b, c}] // Multicolumn[#, 3] &

Multicolumn[
 ReplaceAll[{{} -> "-", p : {(a | b | c) ..} :> StringRiffle[p, ""]}]@
  binLists[{a, b, c}], 
 3]

Use 2 bins:

Multicolumn[
 ReplaceAll[{{} -> "-", p : {(a | b | c) ..} :> StringRiffle[p, ""]}]@
  binLists[{a, b, c}, 2], 
 4]

Use 4 bins:

Multicolumn[
 ReplaceAll[{{} -> "-", p : {(a | b | c) ..} :> StringRiffle[p, ""]}]@
  binLists[{a, b, c}, 4], 
 8]

Use input list {a,b,c,d}:

Multicolumn[
 ReplaceAll[{{} -> "-", p : {(a | b | c | d) ..} :> StringRiffle[p, ""]}]@
  binLists[{a, b, c, d}], 
 10]

Place {a,b,c,d} into 3 bins:

Multicolumn[
 ReplaceAll[{{} -> "-", p : {(a | b | c | d) ..} :> StringRiffle[p, ""]}]@
  binLists[{a, b, c, d}, 3], 
 10]

Place {a,b,c,d} into 2 bins:

Multicolumn[
 ReplaceAll[{{} -> "-", p : {(a | b | c | d) ..} :> StringRiffle[p, ""]}]@
  binLists[{a, b, c, d}, 2], 
 10]

Place {a,b,c,d,e} into 2 bins:

Multicolumn[
 ReplaceAll[{{} -> "-", p : {(a | b | c | d | e) ..} :> StringRiffle[p, ""]}]@
  binLists[{a, b, c, d, e}, 2], 
 10]

kglr · Answer 2 · 2021-10-14T11:36:17.363

partitionQ[l_List][p__List] := DuplicateFreeQ[Flatten@p] && Sort[l] == Union @@ p;

kPartitions[l_List, nbins_Integer] := Select[partitionQ[l]]@Tuples[Subsets @ l, {nbins}]

partitions = kPartitions[{a, b, c}, 3];

Multicolumn[partitions, 3]

Multicolumn[
  ReplaceAll[{{} -> "-", p : {(a | b | c) ..} :> StringRiffle[p, ""]}] @ partitions, 
  3]

Use 4 bins instead of 3:

Multicolumn[
 ReplaceAll[{ {} -> "-", p : {(a | b | c) ..} :> StringRiffle[p, ""]}]@
  kPartitions[{a, b, c}, 4], 
 8]

score 5 · Accepted Answer · answered Oct 14 '21 at 13:19

Make a loop over i1,i2,i3 and put "a" in cell i1, "b" in cell i2 and "c" in i3.

Towards this aim we first define a function that puts "a,b,c" in cells i1,i2,i3:

fun[i1_, i2_, i3_] := Module[{t = {{}, {}, {}}},
  t[[i1]] = Join[t[[i1]], {a}]; t[[i2]] = Join[t[[i2]], {b}]; 
  t[[i3]] = Join[t[[i3]], {c}]; t]

Now it is easy to create the data:

dat = Table[fun[i1, i2, i3], {i1, 3}, {i2, 3}, {i3, 3}];

Finally we may display the data as a Table:

Grid[Flatten[dat, 1], Frame -> All]

Visualizing distribution of 3 balls in 3 cells

3 Answers3