How to solve Coupled a Parabolic and Elliptic PDE in NDSolve?

Question

I want to solve a mixed PDE Parabolic-Elliptic system in 3-dimension (rectangular coordinate), as shown below:

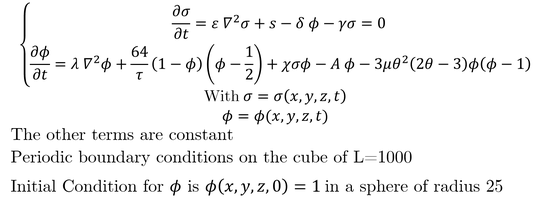
The respective code version with parameters value, boundary and initial conditions is,

    L = 1000;(*length of cube*) 
    pts = 200; 
    T = 400;(*Time integration*) 
    ϵ = 50 λ; 
    s = 2.75; 
    δ = 2.76; 
    γ = 2.75; 
    τ = 3.65; 
    χ = 1.10; 
    A = 1.6438; 
    μ = 0.2; 
    θ = 1; 
    λ = 50;
(*system of nonlinear PDE*) 

pde = {0 == ϵ Laplacian[σ[t,x, y, z], {x, y, z}] + s - δ ϕ[t, x, y, z] - γ σ[t,x, y, z], D[ϕ[t, x, y, z],t] == λ Laplacian[ϕ[t, x, y, z], {x, y, z}] + 64/τ (1 - ϕ[t, x, y, z]) (ϕ[t, x, y, z] - 1/2) + χ σ[t,x, y, z] ϕ[t, x, y, z] - Aϕ[t, x, y, z] - 3 μ θ^2 (2 θ - 3) ϕ[t, x, y, z] (ϕ[t, x, y, z] - 1)}; 

(*Periodic boundary condition*) 

bc = {ϕ[t, 0, y, z] == ϕ[t, L, y, z], ϕ[t, x, 0, z] == ϕ[t, x, L, z], ϕ[t, x, y, 0] == ϕ[t, x, y,L], σ[t, 0, y, z] == σ[t, L, y, z], σ[t, x, 0, z] == σ[t, x, L, z], σ[t, x, y, 0] == σ[t, x, y, L]}; 


(initial condition)
ic = {ϕ[0, x, y, z] == If[(x - 500)^2 + (y - 500)^2 + (z - 500)^2 <= (25)^2, 1, 0]};
eqns = Flatten@{pde, bc, ic};
(Integration)
sol = NDSolve[eqns, {ϕ, σ}, {t, 0, T}, {x, 0, L}, {y, 0, L}, {z, 0, L}, Method -> {"MethodOfLines","SpatialDiscretization" -> {"TensorProductGrid", "MinPoints" -> pts, "MaxPoints" -> pts}}];

but something is not working well.

NDSolve::ivone: Boundary values may only be specified for one independent variable. Initial values may only be specified at one value of the other independent variable.

Can anybody help me?

Thanks in advance.

Answer 1

You can not solve mixed time dependent and stationary equations. You'd have to make the first equation time dependent. Something like this starts to time integrate, though I did not wait for it to finish:

pde = {D[σ[t, x, y, z], t] == ϵ Laplacian[σ[t, x, y, z], {x, y, z}] + 
     s - δ ϕ[t, x, y, z] - γ σ[t, x, y, z], 
   D[ϕ[t, x, y, z], t] == λ Laplacian[ϕ[t, x, y, z], {x, y, z}] + 
     64/τ (1 - ϕ[t, x, y, z]) (ϕ[t, x, y, z] - 
        1/2) + χ σ[t, x, y, z] ϕ[t, x, y, z] - A ϕ[t, x, y, z] - 
     3 μ θ^2 (2 θ - 3) ϕ[t, x, y, z] (ϕ[t, x, y, z] - 1)};
ic = {σ[0, x, y, z] == 0, ϕ[0, x, y, z] == 
    If[(x - 500)^2 + (y - 500)^2 + (z - 500)^2 <= (25)^2, 1, 0]};