When I run the code
DSolve[y*D[f[x, y, z], z] - z*D[f[x, y, z], y] == 0,
f[x, y, z], {x, y, z}]
I get the following output.
I don't understand this syntax. I know c_1 is a function name, but the [x][1/2(y^2+z^2)] throws me off. Does it mean c_1 is a function of two arguments? Is it indicating some sort of product? How am I to understand output of the form f[a][b] in general?
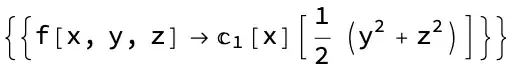
xfrom the independent variables of the PDE, that is, those with respect to which the dependent variables are differentiated. In the way in mathematics $f_a(x)$ represents a family of functions of $x$ depending on a parameter $a$, so does the Mathematica expressionf[a][x]. – Michael E2 Nov 02 '21 at 01:44