4

I can't match the analytical results of a continuous-time Fourier transformation with the results I get from a discrete Fourier transform using Fourier[] in Mathematica.

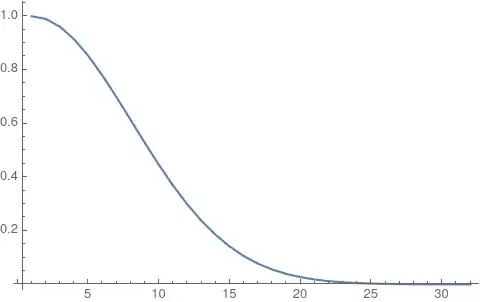
I will try to construct a minimal example in order to illustrate my point. First I generate a discrete set of points from a Gaussian:

data = Table[Exp[-t^2],{t, tmin = 0, tmax = \[Pi], \[CapitalDelta]t = .1}];
ListLinePlot[data, PlotRange -> All]

enter image description here

Following the procedure from this question I right-shift the frequency points in order to centralize the Fourier spectrum. The resulting code for the discrete Fourier transform is:

Nw = Length@data;
wgrid = Table[2 \[Pi] (n - 1) /(\[CapitalDelta]t Nw), {n, -Nw/2 + 1, Nw/2}];                                                         
wgrid = RotateRight[wgrid, Nw/2];                                 
fData = (tmax - tmin)/Sqrt[2 \[Pi] Nw] (Abs@Fourier[data, FourierParameters -> {0, 1}]);

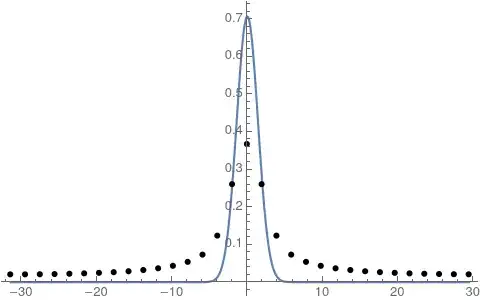
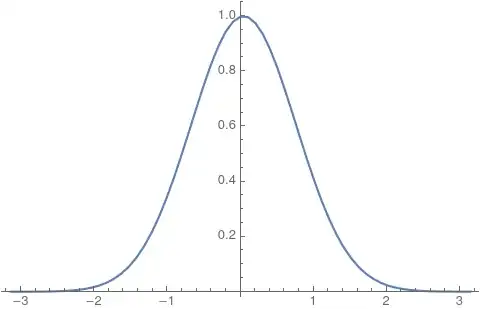
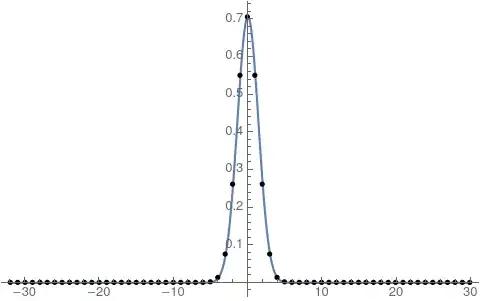
By defining a function for the continous transformation I compare it with the discrete approximation:

cFT[w_] := FourierTransform[Exp[-x^2], x, w, FourierParameters -> {0, 1}];

Show[
 Plot[cFT[w], {w, Min@wgrid, Max@wgrid}, PlotRange -> All],
 ListPlot[Transpose@{wgrid, fData}, PlotRange -> All, PlotStyle -> Black]
 ]

enter image description here

My question is: how can I make these two transformations coincide? I tried several different FourierParameters and normalization factors in fdata, and also different step sizes, but none of them seem to work. The only approach which worked was the one in this question, but I would like to make this work without using HeavisideTheta[] within the Fourier transform.

Gabriel Alves
  • 123
  • 5
  • 3
    Your discrete Fourier transform is of an approximation of a step times a Gaussian, while your continuous Fourier transform is of a Gaussian without the step. So, of course they are different: they are transforms of different functions. FourierParameters can't do anything about this. – John Doty Nov 03 '21 at 13:36
  • @thermans that what I was expecting. Specially given that the results do seem to agree in the linked question (but there they use the Heaviside theta, however). – Gabriel Alves Nov 03 '21 at 14:04
  • 3
    @rhermans But it doesn't approximate the continuous case: there are no points to the left of the peak. Huge difference. – John Doty Nov 03 '21 at 14:15
  • @JohnDoty you're correct, I feel silly now. rhermans I will add an answer to my own question so you can check whether it makes sense or not if you feel inclined to do so. Thank you both of you for your input, I can't believe I overlook such a silly detail. – Gabriel Alves Nov 03 '21 at 14:23

1 Answers1

4

Thanks to @JohnDoty and @rhermans I figured out the problem. The code itself seems ok, the problem is purely mathematical. I generated the data only for positive points, that's why only the approach which uses HeavisideTheta[] works. If I instead generate points symmetrically, for both positive and negative $t$, then the code works.

Generating the data as:

data = Table[Exp[-t^2], {t, tmin = -\[Pi], tmax = \[Pi], \[CapitalDelta]t =.1}];
ListLinePlot[data, PlotRange -> All, DataRange -> {tmin, tmax}]

enter image description here

and using

Nw = Length@data;
wgrid = Table[2 \[Pi] (n - 1) /(\[CapitalDelta]t Nw), {n, -(Nw - 1)/2, (Nw -1)/2}];                                                         
wgrid = RotateRight[wgrid, (Nw - 1)/2];                                 
fData = (tmax - tmin)/Sqrt[2 \[Pi] Nw] (Abs@Fourier[data, FourierParameters -> {0, 1}]);

Clear[cFT];
cFT[w_] := FourierTransform[Exp[-x^2], x, w, FourierParameters -> {0, 1}];


Show[
 Plot[cFT[w], {w, Min@wgrid, Max@wgrid}, PlotRange -> All],
 ListPlot[Transpose@{wgrid, fData}, PlotRange -> All, 
  PlotStyle -> Black]
 ]

we get the correct result:

enter image description here

P.S: Note that some small modifications were made since the number of points is now odd.

Gabriel Alves
  • 123
  • 5