Strange behavior of NDSolve (Error NDSolve::ntdvdae)

Question

i discovered a weird behavior using ```NDSolve``` to solve a set of differential equations.

Let me outline my problem:
I need to solve a set of differential equations. These are equations of motion where the number of equations is depending on the number of shape functions i use.
If i use 8 shape functions i'll get a set of 8 differential equations which NDSolve is evaluating. So there are 8 generalized coordinates (from Subscript[qq, 1][t] to Subscript[qq, 8][t]) which need to be solved via NDSolve.
If i switch the number of shape functions to 9 which means i'll get 9 equations to solve, the NDSolve function is reporting the error message NDSolve::ntdvdae: Cannot solve to find an explicit formula for the derivatives. NDSolve will try solving the system as differential-algebraic equations.
(Please find the list of 8 and the list of 9 equations below to copy paste it into Mathematica. Furthermore i added the syntax i used for solving these equations. See also the initial conditions below in the code.)
(I use Version 12.1.1.0)

Since i need to solve it for 9 (or more) shape functions/equations i wanted to ask you guys if anybody can please help me fixing my problem? I looked it up on the internet but have no idea on how to fix it and i really appreciate any hint of you guys ;-)

Here's the list with 8 equations to solve

ListDGL8={-129.006137732798*Sin[334.7356174047985*t] + 
16038.147354412993*Subscript[qq, 1][t] + 
8019.073677207725*Subscript[qq, 2][t] + 
6961.710838517229*Subscript[qq, 3][t] + 
      6433.029419170023*Subscript[qq, 4][t] + 
6085.362833097541*Subscript[qq, 5][t] + 
5828.203660787876*Subscript[qq, 6][t] + 
5627.085115515234*Subscript[qq, 7][t] + 
      5464.773786742095*Subscript[qq, 8][t] + 
0.12299999999999997*Derivative[2][Subscript[qq, 1]][t] + 
0.06149999999999988*Derivative[2][Subscript[qq, 2]][t] + 
      0.035142857142857226*Derivative[2][Subscript[qq, 3]][t] + 
0.021964285714285738*Derivative[2][Subscript[qq, 4]][t] + 
0.014642857142857091*Derivative[2][Subscript[qq, 5]][t] + 
      0.010250000000000066*Derivative[2][Subscript[qq, 6]][t] + 
0.0074545454545454*Derivative[2][Subscript[qq, 7]][t] + 
0.005590909090909075*Derivative[2][Subscript[qq, 8]][t] == 0, 
  -64.50306886639892*Sin[334.7356174047985*t] + 
8019.073677206336*Subscript[qq, 1][t] + 
12830.008260286922*Subscript[qq, 2][t] + 
12301.32684094079*Subscript[qq, 3][t] + 
      11550.385255502828*Subscript[qq, 4][t] + 
10889.951086133398*Subscript[qq, 5][t] + 
10344.260387403454*Subscript[qq, 6][t] + 
9896.079764234863*Subscript[qq, 7][t] + 
      9525.500273098965*Subscript[qq, 8][t] + 
0.0615*Derivative[2][Subscript[qq, 1]][t] + 
0.03514285714285714*Derivative[2][Subscript[qq, 2]][t] + 
      0.021964285714285714*Derivative[2][Subscript[qq, 3]][t] + 
0.014642857142857124*Derivative[2][Subscript[qq, 4]][t] + 
0.010250000000000037*Derivative[2][Subscript[qq, 5]][t] + 
      0.007454545454545436*Derivative[2][Subscript[qq, 6]][t] + 
0.005590909090909091*Derivative[2][Subscript[qq, 7]][t] + 
0.004300699300699318*Derivative[2][Subscript[qq, 8]][t] == 0, 
  -36.656551732634455*Sin[334.7356174047985*t] + 
6961.710838516545*Subscript[qq, 1][t] + 
12301.326840942595*Subscript[qq, 2][t] + 
14022.914961281625*Subscript[qq, 3][t] + 
      14397.108145685284*Subscript[qq, 4][t] + 
14318.736070694373*Subscript[qq, 5][t] + 
14083.571128609241*Subscript[qq, 6][t] + 
13802.756401830295*Subscript[qq, 7][t] + 
      13520.571185562003*Subscript[qq, 8][t] + 
0.03514285714285714*Derivative[2][Subscript[qq, 1]][t] + 
0.021964285714285714*Derivative[2][Subscript[qq, 2]][t] + 
      0.014642857142857124*Derivative[2][Subscript[qq, 3]][t] + 
0.010250000000000037*Derivative[2][Subscript[qq, 4]][t] + 
0.007454545454545436*Derivative[2][Subscript[qq, 5]][t] + 
      0.005590909090909091*Derivative[2][Subscript[qq, 6]][t] + 
0.004300699300699318*Derivative[2][Subscript[qq, 7]][t] + 
0.003379120879120845*Derivative[2][Subscript[qq, 8]][t] == 0, 
  -22.733293165752244*Sin[334.7356174047985*t] + 
6433.029419171642*Subscript[qq, 1][t] + 
11550.385255508896*Subscript[qq, 2][t] + 
14397.108145690378*Subscript[qq, 3][t] + 
      15694.295645717299*Subscript[qq, 4][t] + 
16267.381548618549*Subscript[qq, 5][t] + 
16480.82839766756*Subscript[qq, 6][t] + 
16509.967514004966*Subscript[qq, 7][t] + 
      16444.178366731503*Subscript[qq, 8][t] + 
0.021964285714285714*Derivative[2][Subscript[qq, 1]][t] + 
0.014642857142857124*Derivative[2][Subscript[qq, 2]][t] + 
      0.010250000000000037*Derivative[2][Subscript[qq, 3]][t] + 
0.007454545454545436*Derivative[2][Subscript[qq, 4]][t] + 
0.005590909090909091*Derivative[2][Subscript[qq, 5]][t] + 
      0.004300699300699318*Derivative[2][Subscript[qq, 6]][t] + 
0.003379120879120845*Derivative[2][Subscript[qq, 7]][t] + 
0.0027032967032967203*Derivative[2][Subscript[qq, 8]][t] == 0, 
  -15.02696945487861*Sin[334.7356174047985*t] + 
6085.362831948756*Subscript[qq, 1][t] + 
10889.951086136134*Subscript[qq, 2][t] + 
14318.736070694926*Subscript[qq, 3][t] + 
      16267.381548612495*Subscript[qq, 4][t] + 
17397.880350381078*Subscript[qq, 5][t] + 
18054.639540893724*Subscript[qq, 6][t] + 
18428.607549193897*Subscript[qq, 7][t] + 
      18629.97845286259*Subscript[qq, 8][t] + 
0.014642857142857124*Derivative[2][Subscript[qq, 1]][t] + 
0.010250000000000037*Derivative[2][Subscript[qq, 2]][t] + 
      0.007454545454545436*Derivative[2][Subscript[qq, 3]][t] + 
0.005590909090909091*Derivative[2][Subscript[qq, 4]][t] + 
0.004300699300699318*Derivative[2][Subscript[qq, 5]][t] + 
      0.003379120879120845*Derivative[2][Subscript[qq, 6]][t] + 
0.0027032967032967203*Derivative[2][Subscript[qq, 7]][t] + 
0.0021964285714285714*Derivative[2][Subscript[qq, 8]][t] == 0, 
  -10.429113172009295*Sin[334.7356174047985*t] + 
5828.203660786874*Subscript[qq, 1][t] + 
10344.26038740584*Subscript[qq, 2][t] + 
14083.571128609183*Subscript[qq, 3][t] + 
      16480.82839766034*Subscript[qq, 4][t] + 
18054.639540892793*Subscript[qq, 5][t] + 
19102.808844437823*Subscript[qq, 6][t] + 
19807.616279822425*Subscript[qq, 7][t] + 
      20283.79973727325*Subscript[qq, 8][t] + 
0.010250000000000037*Derivative[2][Subscript[qq, 1]][t] + 
0.007454545454545436*Derivative[2][Subscript[qq, 2]][t] + 
      0.005590909090909091*Derivative[2][Subscript[qq, 3]][t] + 
0.004300699300699318*Derivative[2][Subscript[qq, 4]][t] + 
0.003379120879120845*Derivative[2][Subscript[qq, 5]][t] + 
      0.0027032967032967203*Derivative[2][Subscript[qq, 6]][t] + 
0.0021964285714285714*Derivative[2][Subscript[qq, 7]][t] + 
0.0018088235294117516*Derivative[2][Subscript[qq, 8]][t] == 0, 
  -7.5222261315258265*Sin[334.7356174047985*t] + 
5627.085115509573*Subscript[qq, 1][t] + 
9896.079764229798*Subscript[qq, 2][t] + 
13802.756401820458*Subscript[qq, 3][t] + 
      16509.96751398605*Subscript[qq, 4][t] + 
18428.60754918051*Subscript[qq, 5][t] + 
19807.616279809037*Subscript[qq, 6][t] + 
20810.86977714626*Subscript[qq, 7][t] + 
      21548.654009568505*Subscript[qq, 8][t] + 
0.007454545454545436*Derivative[2][Subscript[qq, 1]][t] + 
0.005590909090909091*Derivative[2][Subscript[qq, 2]][t] + 
      0.004300699300699318*Derivative[2][Subscript[qq, 3]][t] + 
0.003379120879120845*Derivative[2][Subscript[qq, 4]][t] + 
0.0027032967032967203*Derivative[2][Subscript[qq, 5]][t] + 
      0.0021964285714285714*Derivative[2][Subscript[qq, 6]][t] + 
0.0018088235294117516*Derivative[2][Subscript[qq, 7]][t] + 
0.0015073529411764874*Derivative[2][Subscript[qq, 8]][t] == 0, 
  -5.597559240622573*Sin[334.7356174047985*t] + 
5464.773801028572*Subscript[qq, 1][t] + 
9525.500273096026*Subscript[qq, 2][t] + 
13520.571185554669*Subscript[qq, 3][t] + 
      16444.178366715205*Subscript[qq, 4][t] + 
18629.97845285246*Subscript[qq, 5][t] + 
20283.799737262772*Subscript[qq, 6][t] + 
21548.65400957316*Subscript[qq, 7][t] + 
      22526.08801129856*Subscript[qq, 8][t] + 
0.005590909090909091*Derivative[2][Subscript[qq, 1]][t] + 
0.004300699300699318*Derivative[2][Subscript[qq, 2]][t] + 
      0.003379120879120845*Derivative[2][Subscript[qq, 3]][t] + 
0.0027032967032967203*Derivative[2][Subscript[qq, 4]][t] + 
0.0021964285714285714*Derivative[2][Subscript[qq, 5]][t] + 
      0.0018088235294117516*Derivative[2][Subscript[qq, 6]][t] + 
0.0015073529411764874*Derivative[2][Subscript[qq, 7]][t] + 
0.0012693498452012453*Derivative[2][Subscript[qq, 8]][t] == 0};

Here's the list with 9 equations to solve

ListDGL9={-129.006137732798*Sin[334.73556652336856*t] + 
16038.147354411205*Subscript[qq, 1][t] + 
8019.073677208609*Subscript[qq, 2][t] + 
6961.710838517458*Subscript[qq, 3][t] + 
      6433.029418026366*Subscript[qq, 4][t] + 
6085.362832099767*Subscript[qq, 5][t] + 
5828.2036607934715*Subscript[qq, 6][t] + 
5627.085123744895*Subscript[qq, 7][t] + 
      5464.773809254926*Subscript[qq, 8][t] + 
5331.03754389986*Subscript[qq, 9][t] + 
0.12299999999999997*Derivative[2][Subscript[qq, 1]][t] + 
      0.06149999999999988*Derivative[2][Subscript[qq, 2]][t] + 
0.035142857142857226*Derivative[2][Subscript[qq, 3]][t] + 
0.021964285714285738*Derivative[2][Subscript[qq, 4]][t] + 
      0.014642857142857091*Derivative[2][Subscript[qq, 5]][t] + 
0.010250000000000066*Derivative[2][Subscript[qq, 6]][t] + 
0.0074545454545454*Derivative[2][Subscript[qq, 7]][t] + 
      0.005590909090909075*Derivative[2][Subscript[qq, 8]][t] + 
0.00430069930069936*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -64.50306886639892*Sin[334.73556652336856*t] + 
8019.0736772033815*Subscript[qq, 1][t] + 
12830.008260288385*Subscript[qq, 2][t] + 
12301.326840941168*Subscript[qq, 3][t] + 
      11550.385255510206*Subscript[qq, 4][t] + 
10889.95108613008*Subscript[qq, 5][t] + 
10344.26038741265*Subscript[qq, 6][t] + 
9896.079764221562*Subscript[qq, 7][t] + 
      9525.500273072714*Subscript[qq, 8][t] + 
9216.11355334177*Subscript[qq, 9][t] + 
0.06149999999999988*Derivative[2][Subscript[qq, 1]][t] + 
      0.035142857142857226*Derivative[2][Subscript[qq, 2]][t] + 
0.021964285714285738*Derivative[2][Subscript[qq, 3]][t] + 
0.014642857142857091*Derivative[2][Subscript[qq, 4]][t] + 
      0.010250000000000066*Derivative[2][Subscript[qq, 5]][t] + 
0.0074545454545454*Derivative[2][Subscript[qq, 6]][t] + 
0.005590909090909075*Derivative[2][Subscript[qq, 7]][t] + 
      0.00430069930069936*Derivative[2][Subscript[qq, 8]][t] + 
0.003379120879120816*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -36.656551732634455*Sin[334.73556652336856*t] + 
6961.710838512762*Subscript[qq, 1][t] + 
12301.326840944486*Subscript[qq, 2][t] + 
14022.914961282135*Subscript[qq, 3][t] + 
      14397.108145694714*Subscript[qq, 4][t] + 
14318.736070690153*Subscript[qq, 5][t] + 
14083.571128621115*Subscript[qq, 6][t] + 
13802.75640181324*Subscript[qq, 7][t] + 
      13520.5711855283*Subscript[qq, 8][t] + 
13254.50707224186*Subscript[qq, 9][t] + 
0.035142857142857226*Derivative[2][Subscript[qq, 1]][t] + 
      0.021964285714285738*Derivative[2][Subscript[qq, 2]][t] + 
0.014642857142857091*Derivative[2][Subscript[qq, 3]][t] + 
0.010250000000000066*Derivative[2][Subscript[qq, 4]][t] + 
      0.0074545454545454*Derivative[2][Subscript[qq, 5]][t] + 
0.005590909090909075*Derivative[2][Subscript[qq, 6]][t] + 
0.00430069930069936*Derivative[2][Subscript[qq, 7]][t] + 
      0.003379120879120816*Derivative[2][Subscript[qq, 8]][t] + 
0.002703296703296745*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -22.733293165752244*Sin[334.73556652336856*t] + 
6433.029419167233*Subscript[qq, 1][t] + 
11550.385255511093*Subscript[qq, 2][t] + 
14397.10814569096*Subscript[qq, 3][t] + 
      15694.29564572827*Subscript[qq, 4][t] + 
16267.381548613543*Subscript[qq, 5][t] + 
16480.828397681238*Subscript[qq, 6][t] + 
16509.967513985117*Subscript[qq, 7][t] + 
      16444.178366692387*Subscript[qq, 8][t] + 
16330.908579364535*Subscript[qq, 9][t] + 
0.021964285714285738*Derivative[2][Subscript[qq, 1]][t] + 
      0.014642857142857091*Derivative[2][Subscript[qq, 2]][t] + 
0.010250000000000066*Derivative[2][Subscript[qq, 3]][t] + 
0.0074545454545454*Derivative[2][Subscript[qq, 4]][t] + 
      0.005590909090909075*Derivative[2][Subscript[qq, 5]][t] + 
0.00430069930069936*Derivative[2][Subscript[qq, 6]][t] + 
0.003379120879120816*Derivative[2][Subscript[qq, 7]][t] + 
      0.002703296703296745*Derivative[2][Subscript[qq, 8]][t] + 
0.0021964285714285636*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -15.02696945487861*Sin[334.73556652336856*t] + 
6085.3628319438685*Subscript[qq, 1][t] + 
10889.951086138535*Subscript[qq, 2][t] + 
14318.736070695479*Subscript[qq, 3][t] + 
      16267.381548624719*Subscript[qq, 4][t] + 
17397.880350375548*Subscript[qq, 5][t] + 
18054.639540908975*Subscript[qq, 6][t] + 
18428.60754917178*Subscript[qq, 7][t] + 
      18629.9784528194*Subscript[qq, 8][t] + 
18724.397981297923*Subscript[qq, 9][t] + 
0.014642857142857091*Derivative[2][Subscript[qq, 1]][t] + 
      0.010250000000000066*Derivative[2][Subscript[qq, 2]][t] + 
0.0074545454545454*Derivative[2][Subscript[qq, 3]][t] + 
0.005590909090909075*Derivative[2][Subscript[qq, 4]][t] + 
      0.00430069930069936*Derivative[2][Subscript[qq, 5]][t] + 
0.003379120879120816*Derivative[2][Subscript[qq, 6]][t] + 
0.002703296703296745*Derivative[2][Subscript[qq, 7]][t] + 
      0.0021964285714285636*Derivative[2][Subscript[qq, 8]][t] + 
0.0018088235294117583*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -10.429113172009295*Sin[334.73556652336856*t] + 
5828.20366078161*Subscript[qq, 1][t] + 
10344.260387408489*Subscript[qq, 2][t] + 
14083.571128609881*Subscript[qq, 3][t] + 
      16480.82839767344*Subscript[qq, 4][t] + 
18054.63954088709*Subscript[qq, 5][t] + 
19102.808844453888*Subscript[qq, 6][t] + 
19807.616279798793*Subscript[qq, 7][t] + 
      20283.79973722587*Subscript[qq, 8][t] + 
20605.19607634237*Subscript[qq, 9][t] + 
0.010250000000000066*Derivative[2][Subscript[qq, 1]][t] + 
      0.0074545454545454*Derivative[2][Subscript[qq, 2]][t] + 
0.005590909090909075*Derivative[2][Subscript[qq, 3]][t] + 
0.00430069930069936*Derivative[2][Subscript[qq, 4]][t] + 
      0.003379120879120816*Derivative[2][Subscript[qq, 5]][t] + 
0.002703296703296745*Derivative[2][Subscript[qq, 6]][t] + 
0.0021964285714285636*Derivative[2][Subscript[qq, 7]][t] + 
      0.0018088235294117583*Derivative[2][Subscript[qq, 8]][t] + 
0.001507352941176465*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -7.5222261315258265*Sin[334.73556652336856*t] + 
5627.085115504011*Subscript[qq, 1][t] + 
9896.079764232622*Subscript[qq, 2][t] + 
13802.756401821214*Subscript[qq, 3][t] + 
      16509.96751399996*Subscript[qq, 4][t] + 
18428.607549174223*Subscript[qq, 5][t] + 
19807.61627982615*Subscript[qq, 6][t] + 
20810.869777121115*Subscript[qq, 7][t] + 
      21548.65400951868*Subscript[qq, 8][t] + 
22096.273533439962*Subscript[qq, 9][t] + 
0.0074545454545454*Derivative[2][Subscript[qq, 1]][t] + 
      0.005590909090909075*Derivative[2][Subscript[qq, 2]][t] + 
0.00430069930069936*Derivative[2][Subscript[qq, 3]][t] + 
0.003379120879120816*Derivative[2][Subscript[qq, 4]][t] + 
      0.002703296703296745*Derivative[2][Subscript[qq, 5]][t] + 
0.0021964285714285636*Derivative[2][Subscript[qq, 6]][t] + 
0.0018088235294117583*Derivative[2][Subscript[qq, 7]][t] + 
      0.001507352941176465*Derivative[2][Subscript[qq, 8]][t] + 
0.0012693498452012474*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -5.597559240622573*Sin[334.73556652336856*t] + 
5464.773801022766*Subscript[qq, 1][t] + 
9525.500273098907*Subscript[qq, 2][t] + 
13520.571185555425*Subscript[qq, 3][t] + 
      16444.178366729408*Subscript[qq, 4][t] + 
18629.978452845942*Subscript[qq, 5][t] + 
20283.79973728105*Subscript[qq, 6][t] + 
21548.65400954662*Subscript[qq, 7][t] + 
      22526.08801124734*Subscript[qq, 8][t] + 
23288.863232276402*Subscript[qq, 9][t] + 
0.005590909090909075*Derivative[2][Subscript[qq, 1]][t] + 
      0.00430069930069936*Derivative[2][Subscript[qq, 2]][t] + 
0.003379120879120816*Derivative[2][Subscript[qq, 3]][t] + 
0.002703296703296745*Derivative[2][Subscript[qq, 4]][t] + 
      0.0021964285714285636*Derivative[2][Subscript[qq, 5]][t] + 
0.0018088235294117583*Derivative[2][Subscript[qq, 6]][t] + 
0.001507352941176465*Derivative[2][Subscript[qq, 7]][t] + 
      0.0012693498452012474*Derivative[2][Subscript[qq, 8]][t] + 
0.001078947368421073*Derivative[2][Subscript[qq, 9]][t] == 0, 
  -4.2742528997234785*Sin[334.73556652336856*t] + 
5331.037487920821*Subscript[qq, 1][t] + 
9216.113553331204*Subscript[qq, 2][t] + 
13254.507072221313*Subscript[qq, 3][t] + 
      16330.908579346724*Subscript[qq, 4][t] + 
18724.397981263348*Subscript[qq, 5][t] + 
20605.19607633236*Subscript[qq, 6][t] + 
22096.273533398286*Subscript[qq, 7][t] + 
      23288.863232202362*Subscript[qq, 8][t] + 
24251.03528175503*Subscript[qq, 9][t] + 
0.00430069930069936*Derivative[2][Subscript[qq, 1]][t] + 
      0.003379120879120816*Derivative[2][Subscript[qq, 2]][t] + 
0.002703296703296745*Derivative[2][Subscript[qq, 3]][t] + 
0.0021964285714285636*Derivative[2][Subscript[qq, 4]][t] + 
      0.0018088235294117583*Derivative[2][Subscript[qq, 5]][t] + 
0.001507352941176465*Derivative[2][Subscript[qq, 6]][t] + 
0.0012693498452012474*Derivative[2][Subscript[qq, 7]][t] + 
      0.001078947368421073*Derivative[2][Subscript[qq, 8]][t] + 
0.0009248120300751469*Derivative[2][Subscript[qq, 9]][t] == 0};

This works perfectly

NDSolve[{ListDGL8, Table[Subscript[qq, i][0] == 0, {i, 1, 8, 1}],Table[Subscript[qq, i]'[0] == 0, {i, 1, 8, 1}]},Table[Subscript[qq, i][t], {i, 1, 8, 1}], {t, 0, 0.2}, MaxSteps -> \[Infinity]]

But this doesn't work

NDSolve[{ListDGL9, Table[Subscript[qq, i][0] == 0, {i, 1, 9, 1}],Table[Subscript[qq, i]'[0] == 0, {i, 1, 9, 1}]}, Table[Subscript[qq, i][t], {i, 1, 9, 1}], {t, 0, 0.2}, MaxSteps -> \[Infinity]]

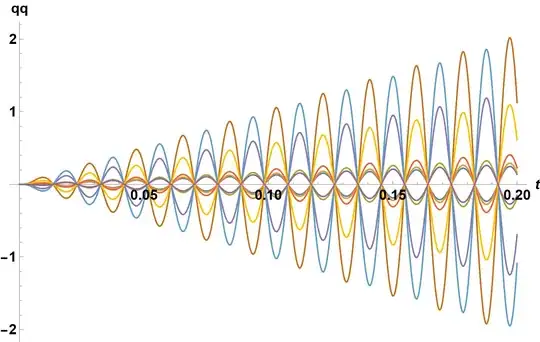
What do you mean by "doesn't work"? Does NDSolve fail after spitting out the warning? If it doesn't, probably it's no more than a warning. At least in v12.3, NDSolve begins solving after the warning, it's just slow. You can use the tool here to monitor t. To understand why the warning pops up, check this post. — xzczd, Nov 08 '21 at 12:58
Solves the stated problem: NDSolve[Join[ Solve[ode9, Variables[ode9 /. Equal -> Subtract][[-9 ;;]]] /. Rule -> Equal, Thread[ Variables[ode9 /. Equal -> Subtract][[-18 ;; -10]] == 1 /. t -> 0], Thread[ D[Variables[ode9 /. Equal -> Subtract][[-18 ;; -10]], t] == 0 /. t -> 0] ], Variables[ode9 /. Equal -> Subtract][[-18 ;; -10]], {t, 0, 1}] — Michael E2, Nov 08 '21 at 13:20
If you're not familiar with what differential-algebraic systems are, and how they differ from conventional differential systems, here are some descriptions of them and how Mathematica solves them for DSolve and for NDSolve. — Michael Seifert, Nov 08 '21 at 13:51
@xzczd I mean there is this warning and there is no result, even if i add the tool you suggested or add the "Method" you sent me a link. I don't get it. In the case of 9 shape functions there is just one additional equation as well as an additional term in every previous equation. I am not able to solve this system of ODE's for more than 8 shape functions. Do you have any idea what the problem could be? — WM_noob5, Nov 08 '21 at 14:50
@Michael E2 i tried your suggestion but the result seems to be totally different from the result of ode8. Also there is a warning General::stop showing up. — WM_noob5, Nov 08 '21 at 14:56
@Michael Seifert I just wanted to use NDSolve to solve this set of ODE's (wich worked for 8 equations but doesn't for 9). So i wanted to ask you guys what the problem could be that Mathematica doesn't evaluate my list of 9 coupled ordinary differential equations? — WM_noob5, Nov 08 '21 at 15:00
@WM_noob5: Most likely, the list of 9 equations you've provided does not uniquely determine all of the highest-order derivatives. Mathematica will try to put the system into first-order form by solving the equations for $q''_1, q''_2$, etc. But if your equations happen to be linearly dependent on each other (in terms of these highest derivatives), then at least one of these second derivatives will not be uniquely determined, and there will be a constraint on some of the lower derivatives of the system. This would trigger the "DAE" warning that you got. — Michael Seifert, Nov 08 '21 at 15:06
One thing I forgot to ask explicitly: are you sure the system is correct? — xzczd, Nov 08 '21 at 16:04

bbgodfrey · Accepted Answer · 2021-11-09T12:30:58.647

The ListDGL9 system can be integrated by solving for the second derivatives with Reduce and then applying NDSolve.

List @@ Reduce[ListDGL9, Table[Derivative[2][Subscript[qq, n]][t], {n, 9}]]
NDSolveValue[{%, Table[Subscript[qq, i][0] == 0, {i, 9}], 
    Table[Subscript[qq, i]'[0] == 0, {i, 9}]}, 
    Table[Subscript[qq, i][t], {i, 9}], {t, 0, 0.2}, MaxSteps -> \[Infinity]];
Plot[%, {t, 0, 0.2}, PlotRange -> All, ImageSize -> Large, 
    AxesLabel -> {t, qq}, LabelStyle -> {15, Bold, Black}]
(* {Subscript[qq, 1]''[t] == 0. + 851.38 Sin[334.736 t] - 
    2.1330110^8 Subscript[qq, 1][t] + 2.8817910^7 Subscript[qq, 2][t] - 
    1.5251210^8 Subscript[qq, 3][t] - 1.9963310^8 Subscript[qq, 4][t] - 
    2.4006610^8 Subscript[qq, 5][t] - 2.7843310^8 Subscript[qq, 6][t] - 
    3.1515410^8 Subscript[qq, 7][t] - 3.5056110^8 Subscript[qq, 8][t] - 
    3.848610^8 Subscript[qq, 9][t], ... } )

(expressions for the other Subscript[qq, n_]''[t] are qualitatively similar.)

This computation takes only several seconds. The plot is qualitatively similar to that obtained for ListDGL8, although as noted in the question, NDSolve can be used directly to obtain the solution quickly.

Addendum: Alternative Approaches

Replacing

List @@ Reduce[ListDGL9, Table[Derivative[2][Subscript[qq, n]][t], {n, 9}]]

by

Rationalize[ListDGL9, 0]

in my solution above also produces the solution quickly. There are several ways to produce the solution very slowly. For instance, the last line of code in the question works on my computer, although the computation takes nearly 30 minutes.

Strange behavior of NDSolve (Error NDSolve::ntdvdae)

1 Answers1