How can I do vector calculations without telling Mathematica the vector entries?
I have very many arbitrary linear combinations in $\mathbb{R}^3$ which I want to perform some general calculations on (scalar and vector products) and want to use Mathematica to do this (especially for simplifying stuff like very long equations with scalar prodcuts of vector products).
So, I don't want to write for all my vectors stuff like v1={a1,b1,c1} ... vN={aN,bN,cN} and so on, but just want to say v1 ... vN are vectors.
How is this possible?
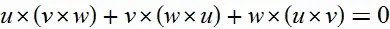
v1={a1,b1,c1}by defining a function, if you don't want to specify this manually. – mmal May 24 '13 at 19:34