2

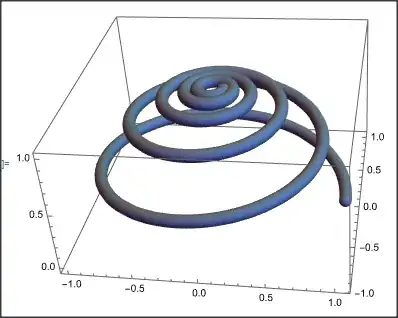
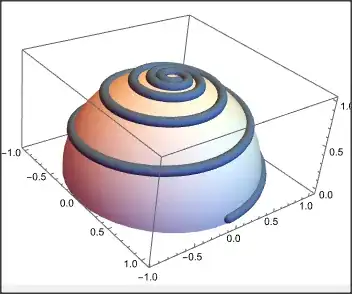
I have the idea to use ResourceFunction["InverseStereographicProjection"] to project various plane curves onto a sphere for the purpose of 3d printing.

This would require that the plane curve has some kind of thickness so that it can be "booleaned" onto the sphere (shell for 3d printing). I thought I could start with the example shown in Wolfram documentation...(https://resources.wolframcloud.com/FunctionRepository/resources/InverseStereographicProjection)

logspiral = 
Entity["PlaneCurve", "LogarithmicSpiral"]["ParametricEquations"][a, 
b][t]
ParametricPlot[
Evaluate[logspiral /. {a -> 1, b -> .1}], {t, 0, 10 \[Pi]}]
sphericalloxodrome = 
ResourceFunction["InverseStereographicProjection"][logspiral] // 
Simplify

I explored this approach in Stereographic Projection in which I attempted to export the orange object but the resulting stl file was not suitable for 3d printing.

What would be the best way to "solidify" the spiral, use it as a cutter and boolean it onto the shell before exporting it as an stl file? I am relatively new to Mathematica and so I hope I can understand any potential responses correctly. Thanks!

shoggananna
  • 205
  • 2
  • 5

1 Answers1

1

I am not sure if I understand "thickness" correctly. I assume that you mean 3D thickness. Then:

fun[a_, b_, t_] = 
 sphericalloxodrome = 
  ResourceFunction["InverseStereographicProjection"][logspiral] // 
   Simplify

curve=ParametricPlot3D[fun[1, 0.1, t], {t, 0, 10 Pi}] /. 
 Line[pts_, rest___] :> Tube[pts, 0.05, rest]

enter image description here

If you want to put this spiral on a sphere you could say:

Show[{curve, Graphics3D[Sphere[]]}]

enter image description here

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
  • Yes you are correct. Then the idea is to project this 3d spiral onto the 3d shell and perform a boolean operation and export as an stl. – shoggananna Nov 13 '21 at 13:16
  • 1
    I hope I interpret correctly what you mean by "project". I added this to my answer. – Daniel Huber Nov 13 '21 at 13:37
  • Well I think the resource function takes care of the projection of the curve from the plane to the sphere? I attempted to cut out the sphere with the spiral cutter via "rr = RegionDifference[reg2, reg1]" where reg2=curve and reg1=fun. Nothing happened. – shoggananna Nov 13 '21 at 14:11
  • Note the Sphere is only the surface, a Ball is the body. – Daniel Huber Nov 13 '21 at 16:21