I try to simplify the function Q below:
Q[x_] := Sign[x] /; x > 1
Simplify[Q[x], Assumptions -> x > 1]
(*return Q[x]*)
But it doesn't work. However, if I write something like this:
Q[x_] := Piecewise[{{Sign[x], x > 1}}]
Simplify[Q[x], Assumptions -> x > 1]
(*return 1*)
It works well. Why is this curious difference? I have searched the documentation but found no help. And is there a third way to write the function Q? I found the double curly braces rather ugly.
Before feeding a function to "Simplify" it will be evaluated. Now, consider:
Clear[Q];
Q[x_] := Sign[x] /; x > 1
Q[x]
(*Q[x]*)
Clear[Q]
Q[x_] := Piecewise[{{Sign[x], x > 1}}]
Q[x]
As you see, the difference is that in the first stage of evaluation Q[x] is not replaced in the first case and replace in the second case.
If you ensure that Q[x] is always replaced it will do what you want. This can be achieved by using "Set" instead of "SetDelayed":
Clear[Q]
Q[x_] = Sign[x] /; x > 1;
Q[x]
Simplify[Q[x], Assumptions -> x > 1]
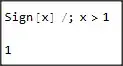
Q[x], there is no value yet forx. So it returns backQ[x]as is. And simplify just seesQ[x]if you replace it withSimplify[Sign[x], Assumptions -> x > 1]then it works because Simplify now seeSign[x]in front of it. – Nasser Nov 15 '21 at 14:16Simplifyknow what's inside.Piecewiseis not what I want, partly because the braces are ugly and partly because it always has a default value. – Adam Page Nov 15 '21 at 14:33Q[x_] := Sign[x]; Simplify[Q[x], Assumptions -> x > 1]because now the call toQ[x]goes through since it is symbolic. When you writeQ[x_/;x>1] := Sign[x]then only whenx>1will the call go through which is not the case. – Nasser Nov 15 '21 at 14:38Q[x_] := Sign[x] /; Simplify[x > 1]; Assuming[x > 1, Simplify[Q[x]]]per the preceding linked question. – Michael E2 Nov 16 '21 at 01:26