10

In a Manipulate, how can a 2D slider be constrained to a specified region — for example, to the unit disk $|z| \leq 1$in the following example?

Manipulate[
   Graphics[{Circle[],
   Line@{{0, 0}, z}, PointSize@Large, Red, Point@z}],
   {{z, {1, 0}}, {-1, -1}, {1, 1}}
]

How constrain 2d slider here to unit disk?

I am aware of how to do this with a Locator, as shown, for example, in answers to Constrain movement of a locator inside Manipulate.

murray
  • 11,888
  • 2
  • 26
  • 50

2 Answers2

13

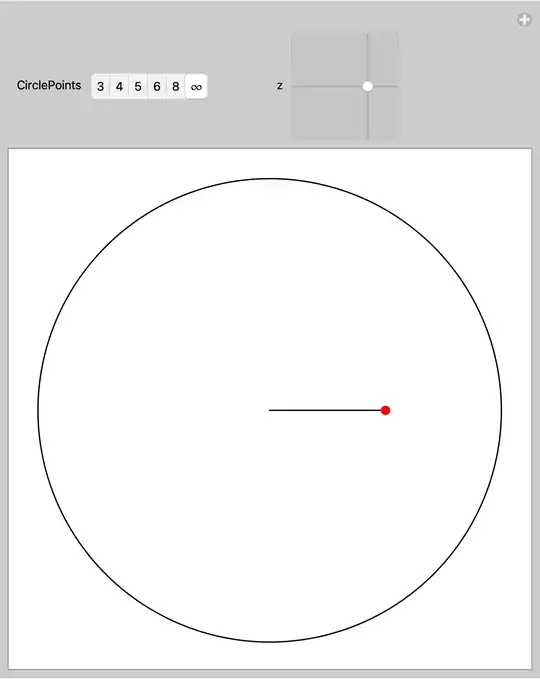
You can use TrackingFunction to restrict the Slider2D thumb to the desired region:

Restrict the thumb to the unit circle:

Manipulate[Graphics[{FaceForm[Opacity[.3]], Blue, Disk[], 
   Black, Circle[{0, 0}, 2], Line@{{0, 0}, z}, 
   PointSize @ Large, Red, Point@z}], 
 {{z, {1, 0}}, {-1, -1}, {1, 1}, TrackingFunction -> ((z = Normalize[#];) &)}]

enter image description here

You can replace ((z = Normalize[#];) &) with ((z = RegionNearest[Circle[]][#];) &) to get the same result.

Use

TrackingFunction -> ((z = If[Norm@# > 1, Normalize[#], #];) &) 
(*or TrackingFunction -> ((z = RegionNearest[Disk[]][#];) &) *)

to restrict the thumb the the unit disk:

enter image description here

Alternatively, add the thumb region as a second control:

regions = Flatten[{RegionBoundary @ #, #} & /@ 
  {Disk[], Rectangle[{-(1/2), -(1/2)}], Triangle[], RegularPolygon[6]}]

icon[size_: 20] := Tooltip[Graphics[{Blue, #}, ImageSize -> 20], #] &;
setters = # -> icon[]@# & /@ regions;


Manipulate[Graphics[{FaceForm[Opacity[.3]], EdgeForm[{Opacity@1, Blue}], Blue, 
   region, 
   Black, Circle[{0, 0}, 2], Line@{{0, 0}, z}, 
   PointSize@Large, Red, Point@z}],
 {{region, Circle[]}, setters, SetterBar, 
  TrackingFunction -> ((region = #; z = RegionNearest[#]@z;) &), 
  Appearance -> "Horizontal" -> {Automatic, 2}},
 {{z, {1, 0}}, {-1, -1}, {1, 1}, 
  TrackingFunction -> ((z = RegionNearest[region]@#;) &), 
  ImageSize -> {100, 100}},
 Method -> "ControlAreaDisplayFunction" -> 
   (Row[Column[#, Alignment -> Center] & /@ #[[1]], Spacer[15]] &)]

enter image description here

Greg Hurst
  • 35,921
  • 1
  • 90
  • 136
kglr
  • 394,356
  • 18
  • 477
  • 896
8
Clear["Global`*"]

$Version

(* "12.3.1 for Mac OS X x86 (64-bit) (June 19, 2021)" *)

Manipulate[Module[{rgn},
  rgn = If[n === Infinity, Disk[],
    Polygon[CirclePoints[n]]];
  z = If[z \[Element] rgn, z, RegionNearest[rgn, z]];
  Graphics[{
    {Opacity[0], EdgeForm[Black],
     rgn},
    Line@{{0, 0}, z},
    PointSize@Large, Red, Point@z}]],
 Row[{
   Control[
    {{n, Infinity, CirclePoints}, {3, 4, 5, 6, 8, Infinity},
     ControlType -> SetterBar}],
   Spacer[50],
   Control[{{z, {1/2, 0}}, {-1, -1}, {1, 1}}]}]]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
  • Suppose we just do the unit disk, thereby removing the control for the type of region. Then why exactly is the Control[z, ...] function explicitly needed, in contrast to the usual form of a Manipulate which just uses {z, ...} ? – murray Nov 24 '21 at 20:25
  • From the docs for Manipulate, "Inside annotations, controls can be specified using Control." and "Possible annotations given in place of controls include expressions with heads String, Style, Row, Item, Text, ExpressionCell, TextCell as well as views and layout constructs such as TabView, Grid, and Multicolumn." If you remove the Row, the Manipulate can be written Manipulate[ ... , {{n, Infinity, CirclePoints}, {3, 4, 5, 6, 8, Infinity}, ControlType -> SetterBar}, {{z, {1/2, 0}}, {-1, -1}, {1, 1}}] – Bob Hanlon Nov 24 '21 at 20:41