I would like to solve the 2D-spatial Allen equation in rectangular coordinate, which is a nonlinear reaction-diffusion PDE of the type
$$\partial_{t}u=\epsilon(\partial_{xx}+\partial_{yy})u + u - u^{3},$$
subject the initial condition $u(x,y,0)=sin(2 \pi x)+0.001cos(16 \pi x)$, where $\epsilon$ is a small but positive constant.
Let's now take the FFT (which include periodic boundary condition) of both sides of the Allen equation to obtain
$$\widehat{\partial_{t}u}_{k} = \epsilon\,(\widehat{\partial^{2}_{xx}u_{k}}+\widehat{+\partial^{2}_{xx}u_{k}})+\widehat{u}_{k}-\widehat{u^{3}}_{k}$$
Where $\widehat{\partial^{2}_{xx}u_{k}}=(i\,k_{x})^{2}\widehat{u}_{k}$ and $\widehat{\partial^{2}_{yy}u_{k}}=(i\,k_{y})^{2}\widehat{u}_{k}$.
Taken into account that nonlinear term $FFT(u^{3}) \neq FFT(u)^3$, so the $u^{3}$ must be computed before taking the FFT. Then,
$$\partial_{t}\widehat{u}_{k} = \epsilon\,((ik_{x})^{2}+(ik_{y})^{2})\,\widehat{u}_{k}+\widehat{u}_{k}-\widehat{u^{3}}_{k}$$
In order to solve this numerically we are going to use a combination of implicit (backward Euler) and explicit (forward Euler) methods (Euler is unstable for this equation). Applying this to Allen equation we find that
$$ \widehat{u}^{n+1}_{k} = \frac{\widehat{u}\,^{n}_{k}(1+1/h)+\widehat{u}_{k}-\widehat{(u^{n})^{3}}_{k}}{-\epsilon\,(ik_{x})^{2}-\epsilon\,(ik_{y})^{2}+1/h}$$
where $k_{x}$ and $k_{y}$ is to remind us that we take the FFT in respected directions. Notice that when programming we are going to have to update the nonlinear term $(u^{3})$ each time you want to calculate the next timestep $n+1$. The reason this is worth mentioning is that for each timestep we are going to have to go from real space to Fourier space to real space, then repeat.
Edit: There is a version of the code in Matlab here.
n = 500;(*Number of discretization points*)
T = 10; (*Time Integration*)
\[Epsilon] = 10^-2; (*diffusivity*)
dt = 10^-2; (*step time*)
kx = I Join[Range[0, n/2 - 1], {0},Range[-n/2 + 1, -1]];(* ik vector in x direction*)
ky = I Join[Range[0, n/2 - 1], {0},Range[-n/2 + 1, -1]];(* ik vector in y direction*)
k2x = kx^2; (*(ik)^2 vector in x direction*)
k2y = ky^2;(*(ik)^2 vector in x direction*)
icu = Table[Sin[2 Pi i] + 0.001 Cos[16 Pi i], {i, n}, {j,n}]; (*initial condition to u*)
ictu = Fourier[icu,FourierParameters -> {1, -1}];(*%FFT for linear*)
icv = Table[Sin[2 Pi i] + 0.001 Cos[16 Pi i], {i,n}, {j,n}]; (*initial condition to u*)
var = Table[{Subscript[u, i, j][t], Subscript[v, i, j][t]}, {i,n}, {j,n}]; (*vector of variables*)
var = Flatten[var]; (*vector of variables*)
eqns = Table[{Subscript[u, i, j][t + 1] == (Subscript[u, i, j][t] (1/dt + 1) - (Subscript[v, i,j][t])^3)/(-\[Epsilon] (k2x[[i, j]] + k2y[[i, j]]) + 1/dt), Subscript[u, i, j][0] == ictu[[i, j]], Subscript[v, i, j][0] == ictv[[i, j]]}, {i, n}, {j, n}];
eqn = Flatten[eqns];
sol = RecurrenceTable[eqn,vars, {t, 0, T}];(*Simulate in real and Fourier frequency domain*)
However I am not getting to update the nonlinear term $(u^{3})$ each time you want to calculate the next timestep n+1. Can anybody help me?
a = Table[InverseFourier[su[[i]]], {i, Length[su]}];
b = Table[{j, l, Re[a[[i, j, l, 1]]]},{i,Length[a]}, {j,Length[a[[i]]]}, {l, Length[a[[i,j]]]}];
c = Table[Flatten[b[[i]], 1], {i, Length[b]}];
Table[ListPlot3D[c[[i]], PlotRange -> All], {i, Length[c]}]
I'm looking for a solution in stationary state like




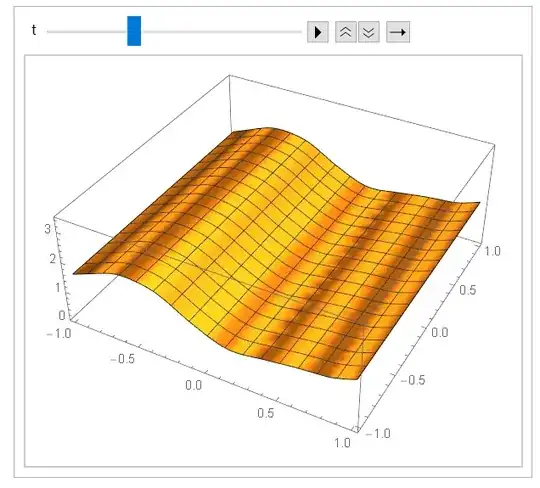
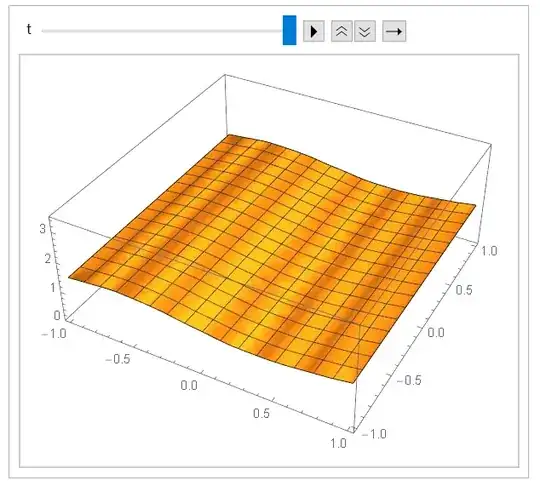
Method->"FiniteElement"solves your problem too! – Ulrich Neumann Nov 25 '21 at 13:16NDSolveasPseudospectralmethod? – xzczd Nov 25 '21 at 13:36NDSolvewithPseudospectral– SAC Nov 25 '21 at 14:58\[Epsilon] = 0.001; Ly = 1; Lx = 1; eq = D[u[t, x, y], t] == Laplacian[u[t, x, y], {x, y}] + u[t, x, y] - u[t, x, y]^3; bc1P = u[t, x, -Ly] == u[t, x, Ly]; bc2P = u[t, -Lx, y] == u[t, Lx, y]; ic = u[0, x, y] == Sin[2 Pi x] + 0.001 Cos[16 Pi x]; mol = {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "DifferenceOrder" -> "Pseudospectral"}}; sol = NDSolve[{eq, bc1P, bc2P, ic}, u, {t, 0, 1}, {x, -Lx, Lx}, {y, -Ly, Ly}, Method -> mol], but it doesn't seem to work. – SAC Nov 25 '21 at 15:00\[Epsilon]is missing in your equation.eqnsis inconsistent with the $\LaTeX$ formula, which one is correct? – xzczd Nov 26 '21 at 02:14\[Epsilon], T andMinPoints->100, but the results of theNDSolveValueorNDSolveobtained by MMA 12 do not reproduce the plot posted in the question. Regarding parameter\[Epsilon], the correct one is in latex. – SAC Nov 26 '21 at 03:43eqnsin the body of question, not theeqin the comment. – xzczd Nov 26 '21 at 15:09