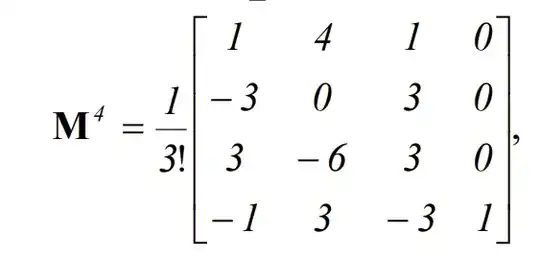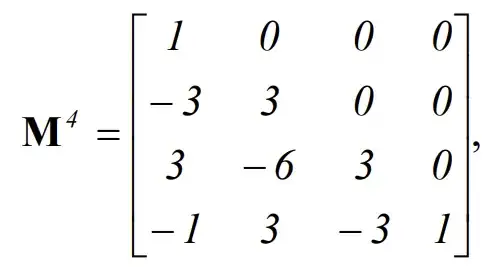3

As we all know, the definition of B-spline contains the B-spline basis function, which has the recursive form enter image description here

$B_{j,k}$ is the j-th degree $k-1$ polynomial. It has nonzeros only in interval $[t_j,t_{j+k})$ which contains $k$ spans $[t_j,t_{j+1}),...,[t_{j+k-1},t_{j+k})$. So for the span $[t_{i},t_{i+1})$ there are in total $k$ degree $k-1$ polynomials. I want to extract the coefficients of every power. These coefficients form a matrix called $M^k(i)$, whose first column number is the coefficients of the first nonzero polynomial $B_{i-k+1,k}$, like this picture: enter image description here

The result for $M^4(i)$ when $t_{i+1}-t_{i}=1$ given in General Matrix Representations for B-Splines, 4.1 Basis matrices of uniform B-splines, is as follows:

enter image description here

In 4.2 Basis matrices for Bezier curves, the matrix is

enter image description here

colth = 0; 
PiecewiseExpand[BSplineBasis[{3, {0, 0, 0, 0, 1, 1, 1, 1}}, colth, x]] 
(*gives the colth column of Basis matrices for Bezier curves *)

How could I get the basis matrices of uniform B-Splines?

Michael E2
  • 235,386
  • 17
  • 334
  • 747
eason
  • 197
  • 5
  • 3
    What have you tried so far? As opposed to just linking to a paper and not asking/hoping that someone will read through it all and give you the result that you are looking for, can you, please, give a bit more background information on this topic? It is not at all clear to me how these matrices relate to the curves in question. – CA Trevillian Dec 07 '21 at 14:24
  • 1
    @CATrevillian I have edited it. Is it ok to reopen ? – eason Dec 08 '21 at 14:14

1 Answers1

7

I'll answer the second one first, since that is relatively straightforward:

The easiest way to get that matrix is

Transpose[Table[CoefficientList[PiecewiseExpand[BernsteinBasis[3, k, x], 0 < x < 1], x],
                {k, 0, 3}]]
   {{1, 0, 0, 0}, {-3, 3, 0, 0}, {3, -6, 3, 0}, {-1, 3, -3, 1}}

which uses the Bernstein basis for Bézier curves. The equivalent B-spline formulation is

Transpose[Table[CoefficientList[PiecewiseExpand[BSplineBasis[{3, {0, 0, 0, 0, 1, 1, 1, 1}}, k, x],
                                                0 < x < 1], x], {k, 0, 3}]]

(exercise: why?)

With that, getting the first matrix only necessitates a change in the knot sequence used. I'll leave as an exercise figuring out where the knot sequence I am using below came from:

Transpose[Table[CoefficientList[
     PiecewiseExpand[BSplineBasis[{3, {-3, -2, -1, 0, 1, 2, 3, 4}}, k, x], 0 < x < 1], x],
     {k, 0, 3}]]
   {{1/6, 2/3, 1/6, 0}, {-1/2, 0, 1/2, 0}, {1/2, -1, 1/2, 0}, {-1/6, 1/2, -1/2, 1/6}}
J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
  • 1
    I have no idea why do so? the paper only requires that $t_{i+1}-t_{i}=1$ ? {-3, -2, -1, 0, 1, 2, 3, 4} why start with -3? and the first 4 are not the same, the last 4 element are not the same ? It seems different form some books . I have another quesion how many control points need to interpolation ? could you recommend me some material or papaer ? – eason Dec 08 '21 at 14:10
  • "why start with -3" - I encourage you to experiment with other knot sequences that satisfy the condition you already stated, and look at what happens to the polynomial expressions generated by PiecewiseExpand[]. As for references, I would recommend Farin's "Curves and Surfaces for Computer-Aided Geometric Design" as a starting point. – J. M.'s missing motivation Dec 09 '21 at 20:08