Is it in general faster to get the eigenvectors and eigenvalues of a dense array rather than a sparse array?

Question

I always thought that things in general go faster when working with sparse array but, I got this:

Eigenvalues::arhm: Because finding 144 out of the 144 eigenvalues and/or eigenvectors is likely to be faster with dense matrix methods, the sparse input matrix will be converted. If fewer eigenvalues and/or eigenvectors at machine precision would be sufficient, consider using N on the matrix and restricting this number using the second argument to Eigenvalues. >>

...do you really, truly, genuinely need all $144$ eigenvalues? Is this matrix symmetric? Structured? What is your actual problem? — J. M.'s missing motivation, May 27 '13 at 18:25
Yes, I need all the eigenvalues, I am trying to get the "Hofstadter-butterfly", so I need to plot all of them. My matrix is Hermititan(self-adjoint). — Mencia, May 27 '13 at 18:32
Yes I had seen it, but here they do it solving "Harper-equation", which I do not, for x reasons ...anyways, it is not too important what I am doing, I just want to know whether it is faster, in general to work with sparsearray or not, since I am using Eigensystem all the time. — Mencia, May 27 '13 at 18:56
Usually in the sparse matrix case, one only wants the biggest few or smallest few, and only very rarely the entire spectrum. If you're asking for a full eigendecomposition, then the effort needed for a sparse array should not be too different from the effort needed for a dense array. — J. M.'s missing motivation, May 27 '13 at 19:00
Sparse methods are not so great for finding most or all eigenvalues, hence the switch to a dense matrix. My guess is that, were "dense" methods applied directly to the sparse form, there would generally be sufficient fill-in as to warrant the switch to an explicit dense form. That said, there are always exceptional cases. — Daniel Lichtblau, Jan 09 '14 at 16:04

score 5 · Accepted Answer · answered Jan 09 '14 at 15:48

From J.M's comment:

Usually in the sparse matrix case, one only wants the biggest few or smallest few, and only very rarely the entire spectrum. If you're asking for a full eigendecomposition, then the effort needed for a sparse array should not be too different from the effort needed for a dense array.

I checked the timing for a few dense and sparse arrays, both with few and with many non-zero elements.

n = 50;
s = SparseArray[
     Append[
      Thread[
       RandomInteger[{1, 144}, {n, 2}] -> RandomInteger[{1, 20}, n]
      ], {i_, i_} -> 1], 
      {144, 144}
     ]

All eigenvalues:

Do[Quiet[Eigenvalues[s]], {1}]; // AbsoluteTiming
t = s // Normal;
Do[Eigenvalues[t], {1}]; // AbsoluteTiming

Only 2 eigenvalues

Do[Quiet[Eigenvalues[s, 2]], {1}]; // AbsoluteTiming
t = s // Normal;
Do[Eigenvalues[t, 2], {1}]; // AbsoluteTiming

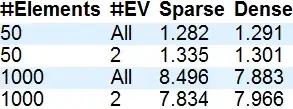
Mathematica graphics

So, not much difference between sparse and dense matrices. Having only a few eigenvalues calculated saves a bit of time but only if the matrix contains many non-zero elements.

Is it in general faster to get the eigenvectors and eigenvalues of a dense array rather than a sparse array?

1 Answers1