ClearAll["Global`*"];
l = 1;
ψ[n_, x_] :=
Exp[-x^2/(2 l^2)] HermiteH[n, x/l]/Sqrt[2^n Factorial[n] Sqrt[Pi] l];
ee[ξ_, x_, Δ0_, Δ1_] :=
Sqrt[ξ^2 +
0.25 l (ψ[0, x] Δ0 + ψ[2,
x] Δ1)^2];
kk[j1_?NumericQ,
j2_?NumericQ, ξ_?NumericQ, Δ0_?
NumericQ, Δ1_?NumericQ] :=
0.125 NIntegrate[ψ[2 j1, x] ψ[2 j2, x]/
ee[ξ, x, Δ0, Δ1], {x, -20, 20}]
ξ = 0.1;
NSolve[{kk[0,
0, ξ, Δ0, Δ1] Δ0 +
kk[0, 1, ξ, Δ0, Δ1] \
Δ1 == Δ0,
kk[1, 0, ξ, Δ0, Δ1] \
Δ0 +
kk[1, 1, ξ, Δ0, Δ1] \
Δ1 == Δ1}, {Δ0, \
Δ1}]
I have checked the above code, I found no problem. It seems Mathematica has not tried to solve it, just return the same expression.
I have tried to solve a simpler equation with only one variable (also have numerical integral), NSolve can handle.
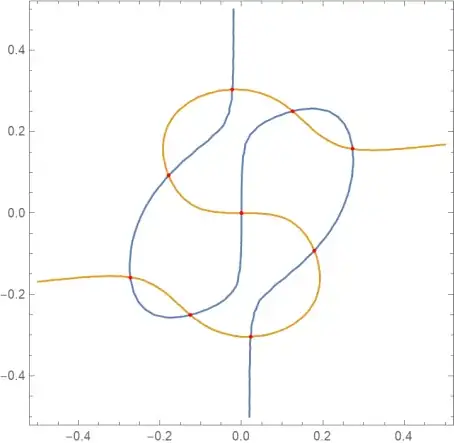
With[{ξ = 0.1}, ContourPlot[{kk[0, 0, ξ, Δ0, Δ1] Δ0 + kk[0, 1, ξ, Δ0, Δ1] Δ1 == Δ0, kk[1, 0, ξ, Δ0, Δ1] Δ0 + kk[1, 1, ξ, Δ0, Δ1] Δ1 == Δ1}, {Δ0, -1/2, 1/2}, {Δ1, -1/2, 1/2}]]seems to indicate that all the roots you are interested in are in the domain shown. – J. M.'s missing motivation Dec 13 '21 at 13:01