5

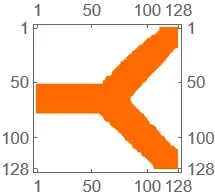
I want to transform a picture into a square matrix with NxN dimension. The elements of the matrix are represented by 0 (red color) or 1 (blue color), from the figure below.

enter image description here

n = 128; (*dimension of matrix*)
f[i_, j_] := (*rule to generated the tube*)
s = SparseArray[{{i_, j_} -> f[i, j]}, {n, n}]; (*matrix*)
MatrixForm[s];

I tried to implement several routines for f[i_,j_], but none of them worked. Can anybody help me?

SAC
  • 1,335
  • 8
  • 17

3 Answers3

7

Since you have the photo already you could just directly convert this into a numeric matrix by copying the image into the "image" placeholder using the code below:

n = 128;
image = Import["https://i.stack.imgur.com/CQkvZ.png"];
image = ImageResize[image, {n,n}];
data = ImageData[ChanVeseBinarize[image]];
MatrixPlot[data]
MatrixPlot[1 - data]

enter image description here enter image description here

This will create a matrix of 1's and 0's where the 0's represent the red pixels and the 1's represent the blue pixels.

AccidentalTaylorExpansion
  • 1,267
  • 6
  • 10
Nate
  • 725
  • 3
  • 14
  • 3
    I find that ChanVeseBinarize[] does a good job of cleaning up the artifacts in the right part of the OP's image. – J. M.'s missing motivation Dec 14 '21 at 19:35
  • Hi @J.M., thanks for the great work. I noticed that in your code, 1's. represents the red pixel and 0's represents the blue pixel. Could you tell me how to change the ordering? Also, how to generate a 128x128 matrix? In other words, how to control the matrix dimension? The matrix generated above has dimension 127x126 – SAC Dec 14 '21 at 21:33
  • 2
    To switch the 1's and 0's you could use: swappedData = data /. {1 -> 0, 0 -> 1} – Nate Dec 14 '21 at 21:41
  • 1 - data should also work for making the swap @SAC wanted. – J. M.'s missing motivation Dec 15 '21 at 06:07
  • 1
    @SAC You can add the line image = ImageResize[image, {n, n}]; inbetween and this will give an output matrix that is n by n. ImageResize migh stretch your image, look at the documentation of ImageResize for ways on how to handle this. – AccidentalTaylorExpansion Dec 15 '21 at 11:01
  • I added that line as an edit – AccidentalTaylorExpansion Dec 15 '21 at 11:08
  • 1
    @AccidentalTaylorExpansion, thank you very much for the suggestion. It was excellent. Thanks for editing the answer. – SAC Dec 15 '21 at 17:29
3

Something like:

n = 128;
n2 = n/2;
del = 15;
f[i_, j_] := Which[
  j < n2 && n2 - del < i < n2 + del, 1,
  n2 <= j && -del < j - i < del, 1,
  n2 <= j && n - del < j + i < n + del, 1,
  True, 0
  ]
s = SparseArray[{{i_, j_} -> f[i, j]}, {n, n}];
MatrixForm[s];
MatrixPlot[s]

enter image description here

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
1

Another approach is to use Colorize...

image = Import["https://i.stack.imgur.com/CQkvZ.png"]
MorphologicalBinarize[image] // Colorize

enter image description here

ImageData[MorphologicalBinarize[image]]

gives the matrix of 0s and 1s.

bill s
  • 68,936
  • 4
  • 101
  • 191