Plotting a 3d curve defined by multiple equations

Question

I am fairly new to mathematica and I am trying to plot a 3D curve defined by multiple formulas. I have the curve $K$ from the point $(\frac{1}{2},-\frac{1}{2}\sqrt{3},0)$ to $(\frac{1}{2},\frac{1}{2}\sqrt{3},2\sqrt{3})$ given by,
$\begin{cases}x^{2}+y^{2}=1,\\ z=\frac{y}{x}+\sqrt{3}\\ x\geq\frac{1}{2} \end{cases}$
I would like to see this curve plotted somehow. I just can't find a function on mathematica which allows this. Does anyone know if this can be done in a simple way?

Answer 1

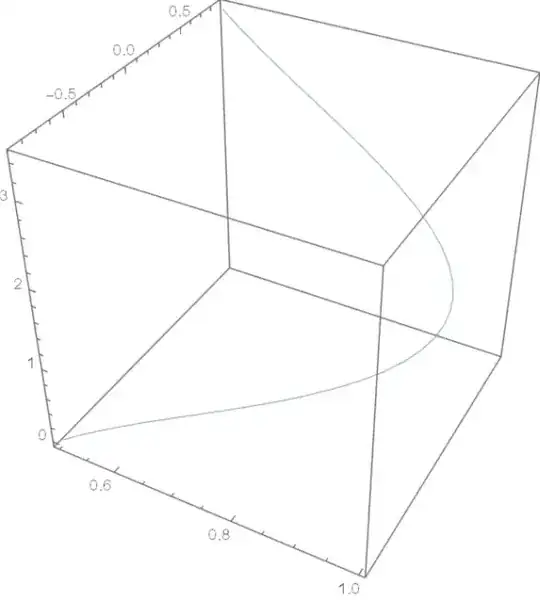
The three conditions define a region

reg = ImplicitRegion[{x^2 + y^2 == 1, z == y/x + Sqrt [3],x > 1/2}, {x, y, z}]

which is plotted with Region

Region[reg, Axes -> True, BoxRatios -> {1, 1, 1}, Boxed -> True]

Answer 2

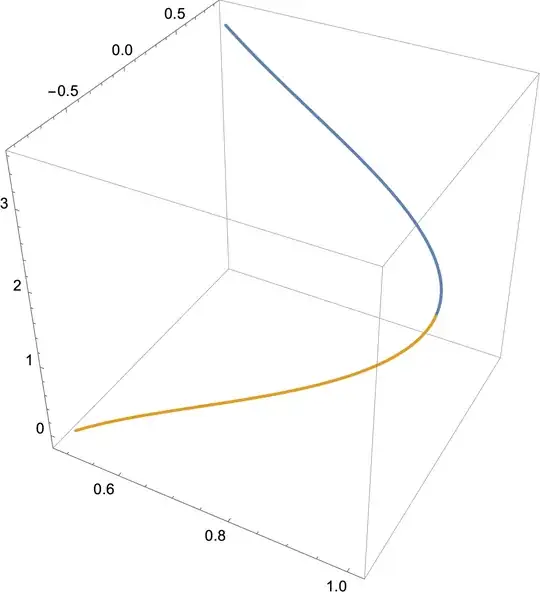
You could also use ParametricPlot3D. The curve is made up of two segments as a function of x

ParametricPlot3D[{
  {x, Sqrt[1 - x^2], Sqrt[1 - x^2]/x + Sqrt[3]},
  {x, -Sqrt[1 - x^2], -Sqrt[1 - x^2]/x + Sqrt[3]}},
 {x, 1/2, 1},
 BoxRatios -> {1, 1, 1}]

Answer 3

Here is an analytical solution:

eq = {x^2 + y^2 == 1 && z == Sqrt[3] + y/x, x > 1/2};
Reduce[eq, z, Reals]

We may take x as a parameter, and plot the 2 branches using ParametricPlot3D:

ParametricPlot3D[{{x, Sqrt[1 - x^2], 
   1/x (Sqrt[3] x + Sqrt[1 - x^2])}, {x, -Sqrt[1 - x^2], 
   1/x (Sqrt[3] x - Sqrt[1 - x^2])}}, {x, 1/2, 1}, 
 BoxRatios -> {1, 1, 1}]

Answer 4

Use the hint by @J.M.can'tdealwithit

sol = Solve[{x == Cos[t], y == Sin[t], z == y/x + Sqrt[3], 
    x >= 1/2, -π <= t <= π},{x,y,z}]
plot = ParametricPlot3D[{x, y, z} /. sol[[1]], {t, -π, π}, 
  PlotStyle -> {Thick, Red}]