1

For instance, I get the following expression:

$\int_0^{\infty } \left(\frac{e^2 x}{e^{2 x+2}-e^{2 x}}-\frac{x}{e^{2 x+2}-e^{2 x}}-\frac{e^2}{2 \left(e^{2 x+2}-e^{2 x}\right)}+\frac{3}{2 \left(e^{2 x+2}-e^{2 x}\right)}+\frac{1}{2}\right) \, dx+\frac{1}{2-2 e^2}$

I want it to be automatically simplified to $\int_0^\infty \frac12 dx$, because all other terms cancel each other (can be verified).

Or $\int_0^{\infty } \left(\frac{3 e^2 x^2}{6 e^x-12 e^{x+1}+6 e^{x+2}}-\frac{6 e x^2}{6 e^x-12 e^{x+1}+6 e^{x+2}}+\frac{3 x^2}{6 e^x-12 e^{x+1}+6 e^{x+2}}-\frac{9 e^2 x}{6 e^x-12 e^{x+1}+6 e^{x+2}}+\frac{24 e x}{6 e^x-12 e^{x+1}+6 e^{x+2}}-\frac{15 x}{6 e^x-12 e^{x+1}+6 e^{x+2}}+x+\frac{e^2}{6 e^x-12 e^{x+1}+6 e^{x+2}}-\frac{8 e}{6 e^x-12 e^{x+1}+6 e^{x+2}}+\frac{13}{6 e^x-12 e^{x+1}+6 e^{x+2}}\right) \, dx+\frac{1}{3}-\frac{1}{1-2 e+e^2}$

should be simplified to $\int_0^\infty x dx$.

Or $\frac{12 e^4 \int_0^{\infty } \left(2 e^{-2 x} x+2 x+\frac{2}{e^{2 x+2}-e^{2 x}}-\frac{e^2}{e^{4 x}+e^{4 x+2}}+\frac{1}{e^{4 x}+e^{4 x+2}}+1\right) \, dx}{12 e^4-12}-\frac{12 \int_0^{\infty } \left(2 e^{-2 x} x+2 x+\frac{2}{e^{2 x+2}-e^{2 x}}-\frac{e^2}{e^{4 x}+e^{4 x+2}}+\frac{1}{e^{4 x}+e^{4 x+2}}+1\right) \, dx}{12 e^4-12}-\frac{e^4}{12 e^4-12}-\frac{18 e^2}{12 e^4-12}-\frac{5}{12 e^4-12}$

should be simplified to $\frac16+2\int_0^\infty x dx+\int_0^\infty 1 dx$.

Is there a way to make Mathematica doing so?

P.S. Input form for the first example:

1/(2 - 2*E^2) + 
 Integrate[
  1/2 + 3/(2*(-E^(2*x) + E^(2 + 2*x))) - 
   E^2/(2*(-E^(2*x) + E^(2 + 2*x))) - 
       x/(-E^(2*x) + E^(2 + 2*x)) + (E^2*x)/(-E^(2*x) + 
      E^(2 + 2*x)), {x, 0, Infinity}]

For the second example:

-(1/3) + 1/(1 - 2*E + E^2) + 
 Integrate[(13*E^x)/(6 - 12*E + 6*E^2) - (8*E^(1 + x))/(6 - 12*E + 
      6*E^2) + 
       E^(2 + x)/(6 - 12*E + 6*E^2) - 
   x + (15*E^x*x)/(6 - 12*E + 6*E^2) - (24*E^(1 + x)*x)/(6 - 12*E + 
      6*E^2) + 
       (9*E^(2 + x)*x)/(6 - 12*E + 6*E^2) + (3*E^x*x^2)/(6 - 12*E + 
      6*E^2) - 
       (6*E^(1 + x)*x^2)/(6 - 12*E + 6*E^2) + (3*E^(2 + x)*x^2)/(6 - 
      12*E + 6*E^2), {x, 0, Infinity}]

For the third example:

-(5/(-12 + 12*E^4)) - (18*E^2)/(-12 + 12*E^4) - E^4/(-12 + 12*E^4) - 
   (12*Integrate[
     1 + 2/(-E^(2*x) + E^(2 + 2*x)) + 1/(E^(4*x) + E^(2 + 4*x)) - 
      E^2/(E^(4*x) + E^(2 + 4*x)) + 
            2*x + (2*x)/E^(2*x), {x, 0, Infinity}])/(-12 + 12*E^4) + 
   (12*E^4*
    Integrate[
     1 + 2/(-E^(2*x) + E^(2 + 2*x)) + 1/(E^(4*x) + E^(2 + 4*x)) - 
      E^2/(E^(4*x) + E^(2 + 4*x)) + 
            2*x + (2*x)/E^(2*x), {x, 0, Infinity}])/(-12 + 12*E^4)

Full code example:

f[x_] := 1 + Exp[-2 x]
g[x_] := 1

omb := D[Sum[
   Refine[DifferenceDelta[Integrate[Integrate[f[t], {t, 0, y}], y], 
      y]*DifferenceDelta[Integrate[Integrate[g[t], {t, 0, y}], y], y],
     y > 0], {y, 0, x - 1}], x]
Func := D[omb, x]; Const := omb /. x -> 0
Inactivate[
    Integrate[f[x], {x, 0, Infinity}][CenterDot]Integrate[
      g[x], {x, 0, Infinity}], Integrate] == 
   FullSimplify[Const + Integrate[Func, {x, 0, Infinity}]] // 
  ExpandAll // Quiet
Anixx
  • 3,585
  • 1
  • 20
  • 32

3 Answers3

5

You might use Distribute[Integrate[Expand[f], {x, 0, Infinity}]], but it seems easier to distribute with Map:

Check[ (* omit Check if not desired *)
 res = 1/(2 - 2*E^2) + 
    Integrate[
     1/2 + 3/(2*(-E^(2*x) + E^(2 + 2*x))) - 
      E^2/(2*(-E^(2*x) + E^(2 + 2*x))) - 
      x/(-E^(2*x) + E^(2 + 2*x)) + (E^2*x)/(-E^(2*x) + 
         E^(2 + 2*x)), {x, 0, Infinity}],
  (** Here's where we distribute Integrate: **)
  res /. 
   HoldPattern[Integrate[f_, x__]] :> With[{terms = Expand[f]},
     Integrate[#, x] & /@ terms /; MatchQ[terms, _Plus]],
  (**                                       **)
  Integrate::idiv] // Simplify

(* Integrate[1/2, {x, 0, Infinity}] *)

Update:

One needs the full linearity of integrals to deal with the OP's problem, and Integrate does not do that. Using linearExpand from another answer we get:

Clear[linearExpand];
linearExpand[e_] := 
  e //. {int : Inactive[Integrate][_Plus, _] :> Distribute[int], 
    Inactive[Integrate][integrand_Times, dom : {x_, _, _} | x_] :> 
     With[{dependencies = 
        Internal`DependsOnQ[#, x] & /@ List @@ integrand}, 
      Pick[integrand, dependencies, False]*
       Inactive[Integrate][Pick[integrand, dependencies, True], dom]]};

linearExpand[Inactive[Integrate][Func // Expand, {x, 0, Infinity}]] //
   Activate // Simplify


(*
  1/(2(-1 + E^2)) +
   (1/2)Integrate[1, {x, 0, Infinity}] + 
   2Integrate[x, {x, 0, Infinity}]
)
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Ah, this seems to work (I didn't trust Distribute not to evaluate Integrate before distributing, and maybe I still shouldn't?): res /. HoldPattern[i : Integrate[f_, x__]] :> With[{terms = Expand[f]}, Distribute[Unevaluated@Integrate[terms, x]] /; MatchQ[terms, _Plus]] – Michael E2 Dec 19 '21 at 16:48
  • Distribute by itself works fine with the result but does not work in the code. – Anixx Dec 19 '21 at 19:53
  • @Anixx I don't know what you mean by "does not work in the code" since it gives me the same result that you said was desired in the OP (except the second example, in which the code is different than the TeX). I guess I'm not sure what "Distribute by itself" means, since I can imagine it being applied correctly or incorrectly. – Michael E2 Dec 19 '21 at 20:32
  • The following code gives the desired answer:FullSimplify[5/(12 - 12*E^2) + E^2/(12 - 12*E^2) + Distribute[Integrate[1/2 + 3/(2*(-E^(2*x) + E^(2 + 2*x))) - E^2/(2*(-E^(2*x) + E^(2 + 2*x))) + 2*x - x/(-E^(2*x) + E^(2 + 2*x)) + (E^2*x)/(-E^(2*x) + E^(2 + 2*x)), {x, 0, Infinity}]]] The problem happens when the integrand is a variable. Inserting "Evaluate" does not help. – Anixx Dec 19 '21 at 20:37
  • This seems to work the way I thought you wanted: Distribute[Integrate[x, {x, 0, Infinity}]]. (Distribute actually does nothing when the integrand is a variable, since the Head of the integrand is not Plus.) – Michael E2 Dec 19 '21 at 21:27
  • I wonder, how can I modify the code so that it to work with integrand being a variable... I want the same result. Can I apply distribute to the second level?... – Anixx Dec 19 '21 at 21:29
  • @Anixx Forgive me, but I guess I'm just slow. If the integrand is just a variable, then isn't the integral exactly this: Integrate[x, {x, 0, Infinity}]? And shouldn't it just remain as is in that case, since it is divergent? – Michael E2 Dec 19 '21 at 21:55
  • I meant expression variable. The code is as follows: FullSimplify[Const + Integrate[Func, {x, 0, Infinity}]] and before that, Func := D[omb, x];. If I add distribute before the Integrate, it does not work. – Anixx Dec 19 '21 at 21:58
  • @Anixx Without a complete working example, I probably cannot help further. Func and its integral evaluate to 0 for me, so there's no problem. I assume that's because omb is not just the symbol omb , but defined to be some else. There seems to be layer after layer followed by yet another unmentioned layer and we've still not arrived at a problem on which Distribute doesn't work. – Michael E2 Dec 19 '21 at 22:23
  • I've added the full code example. – Anixx Dec 19 '21 at 22:28
  • The desired result of the code listed at the end of the OP is $\int_0^{\infty } \frac{1}{2} , dx+\int_0^{\infty } 2 x , dx-\frac{1}{12}$ – Anixx Dec 19 '21 at 22:30
  • @Anixx See my update. I didn't get 1/12. Maybe you could check. – Michael E2 Dec 19 '21 at 23:05
  • In my code the Const term is added. – Anixx Dec 19 '21 at 23:13
  • Your code is sooo complicated. Is there a way to simply make Distribute to work with an expression encoded in variable? – Anixx Dec 19 '21 at 23:15
  • @A Distribute works on expressions of the form f[x1, x2,..] when the head of any of the x1, x2 etc. is Plus. In Distribute[variable], variable is evaluated first, and then Distribute is evaluated. Distribute will work if the expression to which variable evaluates is of the appropriate form. So Distribute always works with an expression encoded in variable; if it seems to fail, it is because of the expression, not because of the variable. (E.g., to get the expression in the appropriate form with the head of an argument to be Plus, one might need Expand or ExpandAll.) – Michael E2 Dec 20 '21 at 01:08
  • Okay, so I made Distribute to sort-of work, but still no simplification and the integrals not cancelled: -(1/12)+(1/2)Integrate[1,{x,0,∞}]+ Integrate[(11x)/(3-3E^2),{x,0,∞}]+ Integrate[(5E^2x)/(3-3E^2),{x,0,∞}]+ Integrate[(5x)/(3E^2-3),{x,0,∞}]+ Integrate[(11E^2x)/(3E^2-3),{x,0,∞}]+ Integrate[-((5x^2)/(E^2-1)),{x,0,∞}]+ Integrate[(5x^2)/(E^2-1),{x,0,∞}]+ Integrate[-((5E^2x^2)/(E^2-1)),{x,0,∞}]+ Integrate[(5E^2x^2)/(E^2-1),{x,0,∞}]+ Integrate[(4x^3)/(3-3E^2),{x,0,∞}]+ Integrate[(4E^2x^3)/(3-3E^2),{x,0,∞}]+ Integrate[(4x^3)/(3E^2-3),{x,0,∞}]+ Integrate[(4E^2x^3)/(3E^2-3),{x,0,∞}] – Anixx Dec 20 '21 at 01:27
  • When applied to the final answer, Distribute cancels all. – Anixx Dec 20 '21 at 01:28
  • Oh, well, finally this worked: added FullSimplify inside Expand: FullSimplify[Const + Distribute[Integrate[ExpandAll[FullSimplify[Func]], {x, 0, Infinity}]]] //ExpandAll // Quiet – Anixx Dec 20 '21 at 01:31
  • All works, so I added my own answer. It is definitely based on your advice and hints, although the solution is different (and I think, simpler). – Anixx Dec 20 '21 at 01:41
0

The first example is fairly easy, the others need more work...

Clear["Global`*"]

conv = a_. + b_. * Inactive[Integrate][integrand_, iter_List] :> 
   Simplify[
    a + Simplify[
      b*Integrate[#, iter] & /@ (integrand // FullSimplify // Expand)]];


Off[Integrate::idiv]


1/(2 - 2E^2) + 
  Inactive[Integrate][
   1/2 + 3/(2(-E^(2x) + E^(2 + 2x))) - E^2/(2(-E^(2x) + E^(2 + 2x))) - 
    x/(-E^(2x) + E^(2 + 2x)) + (E^2x)/(-E^(2x) + E^(2 + 2x)), {x, 0, 
    Infinity}] /. conv

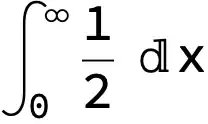
enter image description here

Although it is not clear what this integral tells you that the original didn't: the integral is divergent.

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
0

Well, the trick was to use Distribute outside of Integrate and ExpandAll and FullSimplify inside:

FullSimplify[Const + Distribute[Integrate[ExpandAll[FullSimplify[Func]], 
{x, 0, Infinity}]]] // Quiet

The both FullSimplifys are needed here, as well as ExpandAll inside Integrate.

Full code:

f[x_] := 1 + Exp[-2 x]
g[x_] := 1

omb := D[Sum[
   Refine[DifferenceDelta[Integrate[Integrate[f[t], {t, 0, y}], y], 
      y]*DifferenceDelta[Integrate[Integrate[g[t], {t, 0, y}], y], y],
     y > 0], {y, 0, x - 1}], x]
Func := D[omb, x]; Const := omb /. x -> 0
Inactivate[
   Integrate[f[x], {x, 0, Infinity}][CenterDot]Integrate[
     g[x], {x, 0, Infinity}], Integrate] == 
  FullSimplify[
   Const + Distribute[
     Integrate[
      ExpandAll[FullSimplify[Func]], {x, 0, Infinity}]]] // Quiet

And the result: $\int _0^{\infty }\left(1+e^{-2 x}\right)dx\cdot \int _0^{\infty }1dx=\int_0^{\infty } \frac{1}{2} \, dx+\int_0^{\infty } 2 x \, dx-\frac{1}{12}$

Anixx
  • 3,585
  • 1
  • 20
  • 32