0
G = 3.58;
ϵ = 0.1;
γ = 0.5;
α = 0.5;
η = 0.4;
Subscript[τ, 2] = 9.12;
τ = (2 x)/(2 - ϵ G (Cos[x] + Cos[x]));

ω = (x - τ)/(ϵ τ);

R = Sqrt[4/(9 γ) (Sin[x] + 
      Sin[Subscript[τ, 
         2] + ω ϵ Subscript[τ, 
          2]] + α - η/G)];
m = 2 R;

ParametricPlot[{τ, m}, {x, 0.0001, 500}, Frame -> True, 
 FrameLabel -> {"\!\(\*SubscriptBox[\(τ\), \(1\)]\)", 
   "Amplitude v"}, PlotRange -> {{0, 17}, {0, 3}}, PlotPoints -> 500, 
 PlotStyle -> {Red, Thick}, AspectRatio -> 2/2]
flinty
  • 25,147
  • 2
  • 20
  • 86
Udichi
  • 559
  • 3
  • 13
  • 2
    Don't use Subscript[τ, 2] because τ gets filled in with a value. Use t2 instead. I get a plot after this fix. – flinty Dec 21 '21 at 11:32

1 Answers1

1

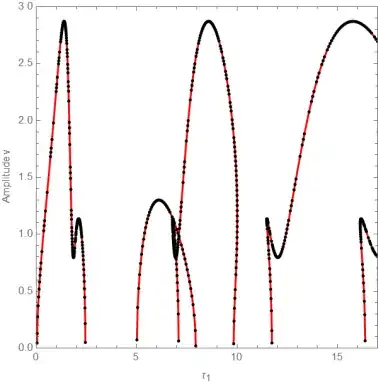
With the @flinty's suggestions you get the values as follows

pic = ParametricPlot[{\[Tau], m}, {x, 0.0001, 500}, Frame -> True, 
FrameLabel -> {"\!\(\*SubscriptBox[\(\[Tau]\), \(1\)]\)", 
"Amplitude v"}, PlotRange -> {{0, 17}, {0, 3}}, PlotPoints -> 500,
PlotStyle -> {Red, Thick}, AspectRatio -> 2/2] ;

[Tau]m = Cases[pic, Line[p_] :> p, Infinity]


Show[{pic, Graphics[Map[Point, [Tau]m]]}]

enter image description here

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55