How can I convert dot product into Latex code without dot?

Question

Recently I need to convert a lot of expressions containing dot products into Latex code. To my annoyance, the mathematica system will always leave literal dots (".") in the latex code, but in reality the dot is mostly omitted in Latex code.

For example, I need to convert this matrix into its latex code:

MatrixForm[{{Transpose[X] . X, Transpose[X] . Subscript[x, 0]}, {Transpose[Subscript[x, 0]] . X, Transpose[Subscript[x, 0]] . Subscript[x, 0]}}]

(Sorry I have to add a picture of the code since the web site keeps notifying me that "Your post appears to contain code that is not properly formatted as code. Please indent all code by 4 spaces using the code toolbar button or the CTRL+K keyboard shortcut. For more editing help, click the [?] toolbar icon. " and prevented me from posting if I contain the original code. I have tried to follow the instructions but nothing has done the trick.)

What I get from directly converting it into Latex code:

But generally, the dot "." generated from dot product is not needed in Latex, what I want is:

Then, how can I tell Mathematica not to generate the dot "." when convert a dot product into its Latex code?

Trying to attach the code in the comment area: MatrixForm[{{Transpose[X] . X, Transpose[X] . Subscript[x, 0]}, {Transpose[Subscript[x, 0]] . X, Transpose[Subscript[x, 0]] . Subscript[x, 0]}}] — AlbertLew, Jan 08 '22 at 09:50
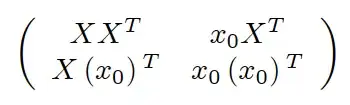
How are you converting to Latex? Using ToString[expr, TeXForm] or TeXForm[expr] or something else? — Carl Woll, Jan 08 '22 at 19:59
@CarlWoll I am used to selecting the expression I would like to convert and right-click on it->Copy As->LaTex — AlbertLew, Jan 10 '22 at 06:38
One thing I have to clarify: the X above is a matrix and x0 above is a vector, so that both of them can be transposed. Product between matrices and/or vectors is not commutative or oderless, namely A B ≠ B A. That's why I have to do it with dot product which does not have the attributes "Orderless" while ordinary product function Times[] has thus it is commutative. As a result, if any proposed solution changes the sequence or order of the product after being converted to Latex code, it is plainly wrong. — AlbertLew, Jan 10 '22 at 07:08

score 5 · Answer 1 · answered Jan 08 '22 at 14:30

5

Try this:

TeXForm[MatrixForm[{{Transpose[X].X, 
     Transpose[X].Subscript[x, 0]}, {Transpose[Subscript[x, 0]].X, 
     Transpose[Subscript[x, 0]].Subscript[x, 0]}}] /. Dot[a_, b_] -> a b]
(* \left(
\begin{array}{cc}
 X X^T & x_0 X^T \
 X \left(x_0\right){}^T & x_0
   \left(x_0\right){}^T \
\end{array}
\right)  *)

wich gives the following

Have fun!

answered Jan 08 '22 at 14:30

Alexei Boulbitch

39,397
2
47
96

Thanks Alexei, but your suggestion does not work since the dot product is not order-less or commutative, terms involved in dot product are usually matrices (like the X above) or vectors( like the x0 above), whose product is not commutative, namely A B ≠ B A. That's why I have to choose dot product which is not order-less doing this rather than ordinary scalar product to do this. But your solution just changed the order/sequence of the product, which might lead to serious mistakes when doing matrices or vectors. – AlbertLew Jan 10 '22 at 06:53
@AlbertLew This you should have specified in your question. Then I would have given you a corresponding solution. Since Carl Woll has already given you a good solution I do not change mine. – Alexei Boulbitch Jan 10 '22 at 08:25
Sorry I did not specify that more clearly at the beginning, since there are superscript T indicating Transpose[] in the expressions. I felt it was clear to signify those are matrices since it is rare to transpose a scalar. But I have already added a comment to clarify it below my post. Hope it does make it more clear. Thanks for your suggestion. – AlbertLew Jan 10 '22 at 09:56

Carl Woll · Answer 2 · 2022-01-12T18:40:23.133

Assuming you're using TeXForm, you could do:

expr = {
    {Transpose[X] . X,Transpose[X] . Subscript[x,0]},
    {Transpose[Subscript[x,0]] . X,Transpose[Subscript[x,0]] . Subscript[x,0]}
};
Block[{Dot},
    Dot /: MakeBoxes[Dot[a_,b_], TraditionalForm] := MakeBoxes[Row[{a,b}],TraditionalForm];
    ToString[expr, TeXForm]
]

$$ \left( \begin{array}{cc} X^TX & X^Tx_0 \\ \left(x_0\right){}^TX & \left(x_0\right){}^Tx_0 \\ \end{array} \right) $$

Update

Another possibility is to use the code from my answer to Change TeXForm of ArcTan, reproduced here:

Initial /: Verbatim[TagSetDelayed][Initial[sym_], lhs_, rhs_] := With[
    {
    new = Block[{sym},
        TagSetDelayed[sym, lhs, rhs];
        First @ Language`ExtendedDefinition[sym, "ExcludedContexts" -> {}]
    ],
    protect = Unprotect[sym]
    },
sym;
Replace[new,
    Rule[values_, n:Except[{}]] :&gt; (
        values[sym] = DeleteDuplicates@Join[n, values[sym]]
    ),
    {2}
];
Protect@protect;

]
Initial[ConvertTeXExpressionToTeX] /: 
    ConvertTeXExpressionToTeX[e__] /; !TrueQ@$TeX := Block[
{$TeX = True},
        ConvertTeXExpressionToTeX[e]
    ]
Initial[Format] /: TagSetDelayed[sym_Symbol, Verbatim[Format][x_, TeXForm], rhs_] := With[
    {fmt = TraditionalForm},
Initial[sym] /: MakeBoxes[x, fmt] /; $TeX := MakeBoxes[rhs, fmt]

]
Initial[Format] /: SetDelayed[Verbatim[Format][x_, TeXForm], rhs_] := With[
    {s = getTagSymbol[Format[x, TeXForm]], fmt = TraditionalForm},
    Replace[s,
        HoldForm[tag_] :> (
            Initial[tag] /: MakeBoxes[x, fmt] /; $TeX := MakeBoxes[rhs, fmt]
        )
    ]
]
SetAttributes[getTagSymbol, HoldFirst]
getTagSymbol[Format[x_, TeXForm]] := Module[{dummy, t},
    extractTag[Hold[Message[Format::tag, HoldForm@Format, , tag], False]] := t = tag;
    Internal`HandlerBlock[{Message, extractTag},
        Quiet[dummy[1] /: Format[x, TeXForm] := 1]
    ];
    t
]

Then, you can define a new TeXForm for Dot:

Format[Dot[a_, b_], TeXForm] := Row[{a, b}]

Now, using "copy as Latex" should also work.

Thanks Carl, your solution does work. However, I wonder how to do it if I am used to converting by the front end instruction "copy as Latex". — AlbertLew, Jan 10 '22 at 07:48

How can I convert dot product into Latex code without dot?

2 Answers2