Is there an easy way in mathematica to approximate $x$ such that $A = \int^{x}_0 f(x) dx$? (where $A$ and $f$ are given)
I am sorry if it is trivial.
Is there an easy way in mathematica to approximate $x$ such that $A = \int^{x}_0 f(x) dx$? (where $A$ and $f$ are given)
I am sorry if it is trivial.
You can do the integration, then use Solve to solve for x
f[x_] := 1 + x + x^2;
A = 10;
int = Integrate[f[t], {t, 0, x}];
eq = A == int

sol = Solve[eq, x]//N
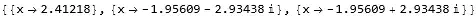
Check:
Integrate[f[t], {t, 0, x /. #}] & /@ sol // Chop
