I need a differential geometry tool for Mathematica. Is there any add-on?
Unfortunately, Mathematica does not include such functionality or I can not find it.
I need a differential geometry tool for Mathematica. Is there any add-on?
Unfortunately, Mathematica does not include such functionality or I can not find it.
Atlas 2 for Mathematica is the add-on for doing modern differential geometry calculations.
The tool is available on DigiArea website and Wolfram Research website. The tool works with Mathematica 8 and Mathematica 9.
First of all in the atlas tool all calculations are coordinate free. That means calculations are performed in terms of tensors, vectors and p-forms. Not their components!
For example conformally flat metric tensor of sphere is presented as:

where  are coframe 1-forms and symbol - tensor product operator.
are coframe 1-forms and symbol - tensor product operator.
Secondly, the package uses standard differential geometry notations for exterior derivative, covariant differentiation, tensor product etc. It is really helpful to see the same results/formulas on the screen and in my textbooks.



Atlas is very user-friendly and doesn't bog down with a lot of programming which is really importance for people interested in learning.
There are a lot of predefined operators to declare various DG objects.
Just for example Invariants operator automatically calculates invariants of a mapping:
The package has Visualize function that visualizes n-dimensional differential geometry objects using different Mathematica plot functions. The function allows quickly visualize an object and its projections. See some examples.
For example visualization of projections for Mobius strip.
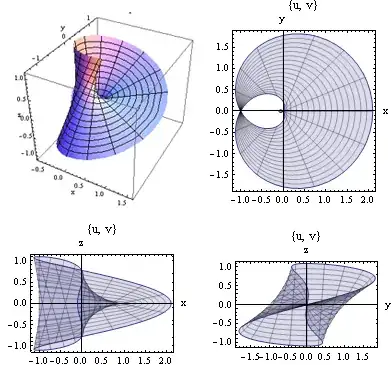
The tool gives access to Differential Geometry Library directly from Mathematica.
The library has over 550 objects for differential geometry and its applications and frequently updated. The are hundreds of Exact Solutions of Einstein's Field Equations and atlas's graphical user interface (see below) allows calculate any of the objects/Exact Solutions just in few seconds.
Currently, the library has 6 categories:
The modern differential geometry is a vast subject and while not specified exactly what you need the question is a bit too general. I would rather point out a few references.
If you are looking for a package for tensor calculus, especially in General Relativity, the best choice is xAct made by José M. Martín-García (as far as I know he actually develops built-in functionality for the future versions of Mathematica):
However if you need something straightforward and concise, look at this implementation below of a few fundamental objects in differential geometry. You need a metric g and a coordinate system xx on an open set of a 4-dimentional (riemannian or lorentzian) manifold (but it is a straightforward to define these objects for other dimentions) as an input, eg.
xx = {t, x, theta, phi};
g = { { -E^(2 nu[x]), 0, 0, 0}, {0, E^(2 lambda[x]), 0, 0},
{0, 0, x^2, 0}, {0, 0, 0, x^2 Sin[theta]^2}};
The above is a Lorentzian metric tensor (in a given map) of a static spherically symmetric four dimentional manifold, and the following are the inverse metric, Christoffel symbol of the second kind, Riemann and Ricci curvature tensors and the Ricci scalar with brief descriptions of their usage:

InverseMetric[ g_, xx_] :=
Block[{ res },
res = Simplify[ Inverse[g] ];
res
]

ChristoffelSymbol[g_, xx_] :=
Block[{n, ig, res},
n = 4;
ig = InverseMetric[ g, xx];
res = Table[(1/2)*Sum[ ig[[i,s]]*(-D[ g[[j,k]], xx[[s]]] +
D[ g[[j,s]], xx[[k]]]
+ D[ g[[s,k]], xx[[j]]]),
{s, 1, n}],
{i, 1, n}, {j, 1, n}, {k, 1, n}];
res
]

RiemannTensor[g_, xx_] :=
Block[{n, Chr, res},
n = 4;
Chr = ChristoffelSymbol[ g, xx];
res = Table[ D[ Chr[[i,k,m]], xx[[l]]]
- D[ Chr[[i,k,l]], xx[[m]]]
+ Sum[ Chr[[i,s,l]]*Chr[[s,k,m]], {s, 1, n}]
- Sum[ Chr[[i,s,m]]*Chr[[s,k,l]], {s, 1, n}],
{i, 1, n}, {k, 1, n}, {l, 1, n}, {m, 1, n}];
res
]

RicciTensor[g_, xx_] :=
Block[{Rie, res, n},
n = 4;
Rie = RiemannTensor[ g, xx];
res = Table[ Sum[ Rie[[ s,i,s,j]],
{s, 1, n}], {i, 1, n}, {j, 1, n}];
res
]

RicciScalar[g_, xx_] :=
Block[{Ricc,ig, res, n},
n = 4;
Ricc = RicciTensor[ g, xx];
ig = InverseMetric[ g, xx];
res = Sum[ ig[[s,i]] Ricc[[s,i]], {s, 1, n}, {i, 1, n}];
Simplify[res]
]
This is not an optimal implementation, but it is a good point to start building your own package. You could think about introducing a functional definition of the covariant derivative as well as lower and upper indices of covariant and contravariant tensors. One of the common difficulties with this is the multiplicity of definitions and conventions for Riemann and Ricci tensors etc, and that's why I added descriptions of the given functions.
Besides of the above I recommend to look at the Wolfram Demonstrations :
e.g.
One should also look at the geometry section of
Next it would be even more helpful and strongly recommended to look at these articles (some of them are particularly devoted to differential geometry topics, others only deal with useful geometric techniques) in the Mathematica Journal :
You may want to look, also, at David Park's Tensorial application as well as the associated TensorForms subpackage. See: http://home.comcast.net/~djmpark/TensorialPage.html
xActpackage for tensor calculus (not only for this) http://www.xact.es, there are big chances that is similar to the future Mathematica built-in functionality. – Artes Mar 07 '12 at 03:06