Convert complex exponential to real exponentials, sines and cosines

Question

While taking the inverse Laplace transform of certain expressions, Mathematica yields complex exponentials. For example, using the following code:

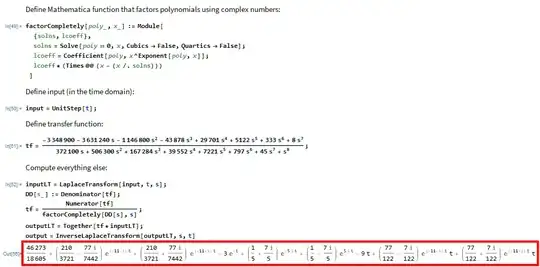
(*Define Mathematica function that factors polynomials using complex numbers (taken from https://mathematica.stackexchange.com/a/10588/71575):*)
factorCompletely[poly_, x_] := Module[
  {solns, lcoeff},
  solns = Solve[poly == 0, x, Cubics -> False, Quartics -> False];
  lcoeff = Coefficient[poly, x^Exponent[poly, x]];
  lcoeff*(Times @@ (x - (x /. solns)))
  ]
(Define input (in the time domain):)
input = UnitStep[t];
(Define transfer function:)
tf = (-3348900 - 3631240 s - 1146800 s^2 - 43878 s^3 + 29701 s^4 + 5122 s^5 + 333 s^6 + 8^7)/(372100 s + 506300 s^2 + 167284 s^3 + 39552 s^4 + 7221 s^5 + 797 s^6 + 45 s^7 + s^8);
(Compute everything else:)
inputLT = LaplaceTransform[input, t, s];
DD[s_] := Denominator[tf];
tf = Numerator[tf]/factorCompletely[DD[s], s];
outputLT = Together[tf*inputLT];
output = InverseLaplaceTransform[outputLT, s, t]

we get:

$\dfrac{46\,273}{18\,605} + \left(\dfrac{210}{3\,721} - j\dfrac{77}{7\,442} \right) e^{(-11 - j1) t} + \left(\dfrac{210}{3\,721} + j \dfrac{77}{7\,442} \right) e^{(-11 + j) t} - 3 e^{-t} + \left(\dfrac{1}{5} + j \dfrac{7}{5} \right) e^{-j 5 t} + \left(\dfrac{1}{5} - j \dfrac{7}{5} \right) e^{j 5 t} - 9 t + \left(\dfrac{77}{122} - j \dfrac{7}{122} \right) e^{(-11 - j) t} t + \left(\dfrac{77}{122} + j \dfrac{7}{122} \right) t e^{(-11 + j) t} \tag 1$

as shown in the following figure:

Figure 1.

However, I'd like to rewrite the complex exponentials as real exponentials, sines and cosines. In this Quora answer I derived a formula for doing such conversion:

$\begin{align} (a + jb) e^{(\sigma_0 \mp j \omega_0)t} + (a - jb) e^{(\sigma_0 \pm j \omega_0)t} &= 2 e^{\sigma_0 t} [a \cos{(\omega_0 t)} \pm b \sin{(\omega_0 t)}] \\ &= 2 \sqrt{a^2 + b^2} e^{\sigma_0 t} \cos{(\omega_0 t \mp \text{atan2}{(b, a)})} \end{align} \tag 2$

But I don't know how to create a Mathematica function that looks for an expression/pattern (the complex exponentials) in another expression (expression (1)) and substitutes it with yet another expression (the right-hand side of (2)). I found this webpage listing various Mathematica functions but couldn't figure out how to use them for my problem.

Answer 1

In this blog post, I showed a method for taking the inverse Laplace transform of a rational function based on a method of Longman and Sharir. To keep this answer self-contained, here's the function from that post:

inverseLaplaceRational[f_, x_] /; Internal`RationalFunctionQ[f, x] := 
       Module[{af, dc, ff, nc, p, q, rs},
              ff = Together[f];
              nc = CoefficientList[Numerator[ff], x];
              dc = CoefficientList[Denominator[ff], x];
              If[Length[nc] >= Length[dc],
                 Return[$Failed, Module]];
              af = Last[dc]; dc = dc/af; nc = nc/af;
              p = Length[nc] - 1; q = Length[dc] - 1;
              rs = ListCorrelate[nc, 
                   LinearRecurrence[-Reverse[Most[dc]],
                                    UnitVector[q, q], 
                                    p + q], {1, -1}];
              DifferentialRoot[Function @@ {{\[FormalY], \[FormalX]}, 
                   Prepend[Thread[Table[Derivative[k][\[FormalY]][0],
                                        {k, 0, q - 1}] == rs], 
                   dc.Table[Derivative[k][\[FormalY]][\[FormalX]],
                            {k, 0, q}] == 0]}]]

Applied to your transfer function:

inverseLaplaceRational[(-3348900 - 3631240 s - 1146800 s^2 - 43878 s^3 + 29701 s^4 +
                        5122 s^5 + 333 s^6 + 8^7)/(372100 s + 506300 s^2 + 167284 s^3 +
                        39552 s^4 + 7221 s^5 + 797 s^6 + 45 s^7 + s^8)/
                       s, s][t] // FunctionExpand // Expand
   -29402639/5674525 + (50057 E^-t)/10201 - (312937 t)/93025 -
   (194982572043520172 E^(-11 t) Cos[t])/1071205248108384661 +
   (3585457782145 E^(-11 t) t Cos[t])/8083533889 +
   (5279489414 Cos[5 t])/11565927025 -
   (484215234928027221145 E^(-11 t) Sin[t])/1071205248108384661 +
   (706657867485 E^(-11 t) t Sin[t])/8083533889 + (170556879482 Sin[5 t])/57829635125

You can check that applying LaplaceTransform[] to that result recovers the original rational function.