I am struggling to understand the Fourier series in Mathematica.
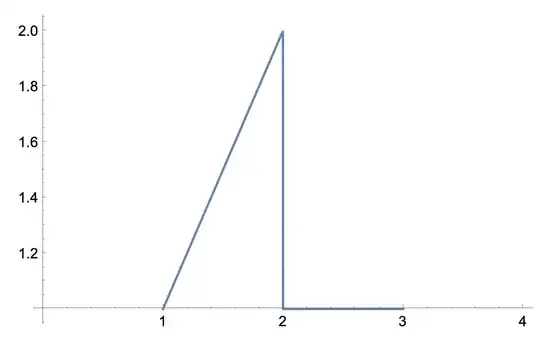
I don't find a way to calculate Fourier series for a general function which is not periodic and defined on a interval but not on typical inervals like [-Pi, Pi] as required by FourierSeries command. For example like a function shown below.
My first naive idea to use FourierParameters option of FourierSeries, but I don't know how to set them.
I search the forum for my problem. I saw the great answer by xzczd who invented easyFourier , but that is too much programming for me.
func[x_] := Piecewise[{{x, 1 <= x < 2}, {1, 2 <= x <= 3}}, Undefined]
Plot[func[x], {x, 0, 4}]
Thanks in advance! :)
======================= Update 1 ============================
Thanks to the helpful comments by xzczd, it seems that the FourierParameters is not feaible to obtain a non-periodic function defined on any interval.
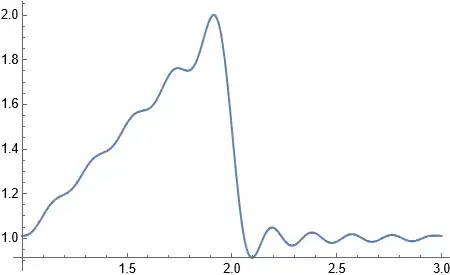
As inspired by @rmw's Rescale method, problem seems to be solved. Thus, now my question changed to "this Rescale based method is general enough? What are its limitations?"
======================= Update 2 ============================
As kindly suggested by @xzczd in the comments, I double checked the easyFourier and find some useful observation.
Beside making Fourier series for an function on genral interval [a, b], the other motivation for making easyFourier by xzczd is that a general form of Fourier series is highly desired,for example, for solving pdes. In this general form, a symbol parameter C, instead of a specific numeric integer, is used to control the order of expansion.
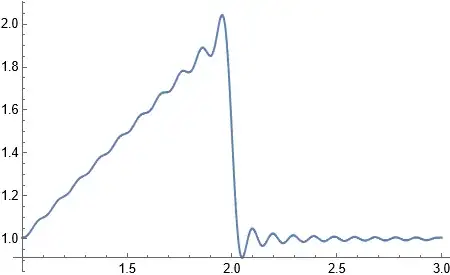
Although, Rescale method as shown by rmw can be used to give Fourier for an fucntion on any interval, it can't gives the general form of Fourier series.
======================= Update 3 ============================
Now, I think I should give another update. rmw gives such a good answer which shows that Rescale method can do what easyFourier aimed to do. Do I understand this Right?
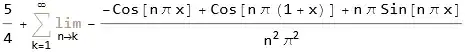
FourierParameter, I won't have createdeasyFourier… Just read the Details and Options section ofFourierSeries, you'll see it's not possible toTranslatewithFourierParameter. – xzczd Jan 13 '22 at 06:05FourierParameters {a,b}not general enough? Can't we just use variable change orRescalemethod as shown by @rmw ? Please, can you show a example whose Fourierseries cannot be obtaiined? Thanks:) – op-luffy Jan 13 '22 at 10:44Rescalealready involves coordinate translation, and this isn't achievable withFourierParameters. Once again, please read the Details and Options section ofFourierSeries. – xzczd Jan 13 '22 at 10:55FourierParametersto realize whatRescaledoes, right? Can't we just useRescalefor general function defined on any interval? For more clearness, I updated the quesion. Thanks for your helpful comments. – op-luffy Jan 13 '22 at 11:04Rescalemethod general enough? I am sure that you must know this method when you makeeasyFourier, then why you made it? Is it becasueRescalemethod has some its limitations? I had naively think my question is similar to your question where I findeasyFourier. – op-luffy Jan 13 '22 at 11:30easyFouriermore carefully. – xzczd Jan 14 '22 at 03:32Rescalemethod can't solve your problem. Do I understandeasyFourierright as stated in update 2? Thanks for your kind and helpful comments. – op-luffy Jan 14 '22 at 04:03