Looking for intuition as to what numerical issue makes this solution of NDSolve blow up unphysically

Question

I am solving the spherically symmetric wave equation in 3 dimensions on $r\in[0,2\pi]$ $$(\partial_t^2 - \frac{1}{r^2} \partial_r r^2 \partial_r) \theta(t,r)=0$$ with initial conditions $\theta(0,r)=e^{-(r-3)^2}$ and $\partial_t\theta(0,r)=0 $, imposing boundary conditions $$\partial_r\theta(t,0)=0, \qquad \partial_t(r\theta)(t,6)+\partial_r(6\theta)(t,6)=0.$$ The first is necessary for smoothness at the origin and the second (necessary to solve on a finite domain) should make sure that no information comes form outside the domain.

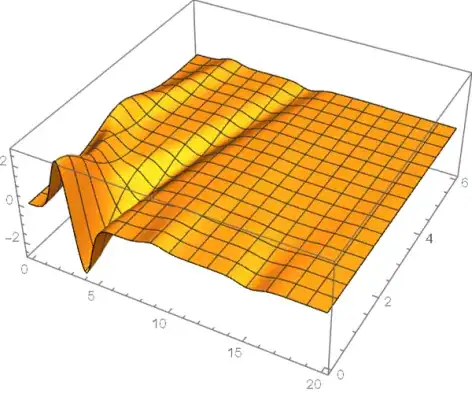
I include my code below. As you will see, the solution behaves reasonable at first and then starts growing for no reason. I would like to gain some intuition as to what numerically is the problem and how to extend the reasonable behaviour time.

tend = 100.;
rstart = 1/10^100;
rend = 6;
eq = D[θ[t, r], {t, 2}] - 1/r^2 D[r^2 D[θ[t, r], r], r] == 0;
ic = {θ[0, r] == Exp[-(r - 3)^2], (D[θ[t, r], t] /. t -> 0) == 0};
bc = {(D[θ[t, r], r] /. r -> rstart) == 
0, (D[r θ[t, r], t] /. r -> rend) + (D[r θ[t, r], r] /. r -> rend) == 0};
sol = NDSolve[Flatten@{eq, ic, bc}, θ, {t, 0, tend}, {r, rstart, rend}]
Animate[Plot[{θ[t, r] /. sol}, {r, rstart, rend}, PlotRange -> {{rstart, rend}, {-2, 2}}], {t, 0, tend}]

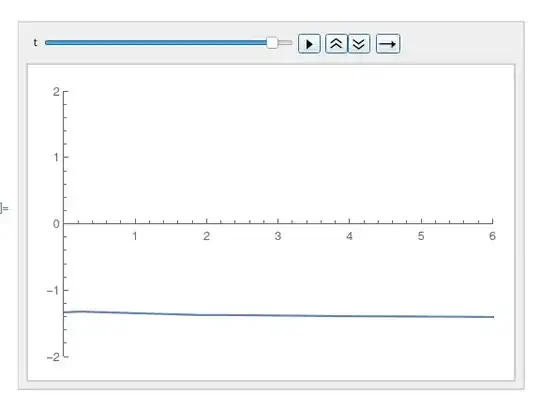
Edit: I'm running version 12.1. Below I include an snapshot of the animation when the solution starts to drift downwards

Does “DifferenceOrder” -> “Pseudospectral” in the spatial discretization help? — Michael E2, Jan 16 '22 at 19:32
“As you will see, the solution behaves reasonable at first and then starts growing for no reason.” I don't seem to see it in v12.3.1, can you add your version info and a picture showing the growing? — xzczd, Jan 17 '22 at 07:05
@xzczd I've added a picture of a timeslice when the solutions starts to go off. My version is 12.1. I hope that helps — Rudyard, Jan 17 '22 at 14:37
Here's the result of v12.3.1: https://i.stack.imgur.com/8STbu.png What if you add Method -> {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 45, "MinPoints" -> 45, "DifferenceOrder" -> 4}, Method -> "Adams"} to NDSolve in v12.1? Also, you may need "DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100}. (To learn more about this option, you can read the following post: https://mathematica.stackexchange.com/a/127411/1871 ) — xzczd, Jan 17 '22 at 14:47
Just tested in v9.0.1, I observed similar phenomenon, and the option combination in my last comment fixes the problem in v9.0.1. A simpler solution is to add MaxStepSize -> {0.05, Automatic}. Do these options work in v12.1? — xzczd, Jan 17 '22 at 15:01
@xzczd adding MaxStepSize -> {0.05, Automatic} prolonged the reasonable behaviour but eventually, around t=500 it goes off again. Your previous suggestion, including the "DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100} option works great! without the last option it also eventually goes off — Rudyard, Jan 18 '22 at 11:14

score 4 · Answer 1 · answered Jan 16 '22 at 16:42

MethodOfLines with FiniteElement gives a more plausible solution:

bc is changed to NeumannValue (first bc is automatically fullfilled)

teta = NDSolveValue [Flatten@{-((2 r \!\(\*SuperscriptBox[\(\[Theta]\), TagBox[RowBox[{"(",RowBox[{"0", ",", "1"}], ")"}],Derivative],MultilineFunction->None]\)[t, r] +r^2\!\(\*SuperscriptBox[\(\[Theta]\),TagBox[RowBox[{"(",RowBox[{"0", ",", "2"}], ")"}],Derivative],MultilineFunction->None]\)[t, r])/r^2) +\!\(\*SuperscriptBox[\(\[Theta]\),TagBox[
RowBox[{"(", RowBox[{"2", ",", "0"}], ")"}],Derivative],MultilineFunction->None]\)[t, r] ==NeumannValue[-Derivative[1, 0][\[Theta]][t, r], r== 6] , ic }, 
\[Theta], {t, 0, tend}, {r, rstart, rend},Method -> {"MethodOfLines", "TemporalVariable" -> t,"SpatialDiscretization" -> {"FiniteElement" ,"MeshOptions" -> { "MaxCellMeasure" -> 0.1} }}]
Plot3D[teta[t, r], {t, 0, tend/5}, {r, rstart,rend}, PlotPoints -> 100, PlotRange -> All]

score 4 · Answer 2 · answered Jan 19 '22 at 01:36

OK, since OP confirms the following solution also works in v12.1, let me turn it into an answer: I observe similar behavior in v9.0.1, and adding

Method -> {"MethodOfLines", 
  "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 45, "MinPoints" -> 45,
                              "DifferenceOrder" -> 4}, 
  "DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100}, Method -> "Adams"}

is a way to resolve the problem. To understand why DifferentiateBoundaryConditions is added, you can read this post.

score 3 · Answer 3 · answered Jan 20 '22 at 00:26

Putting my comment into an answer: "DifferenceOrder" -> "Pseudospectral" seems to work.

sol = NDSolve[
  Flatten@{eq, ic, bc}, θ, {t, 0, tend}, {r, rstart, rend}, 
  Method -> {"MethodOfLines", 
    "SpatialDiscretization" -> {"TensorProductGrid", 
      "DifferenceOrder" -> "Pseudospectral"}}]
Plot3D[θ[t, r] /. sol, {t, 0, tend/5}, {r, rstart, rend}, 
 PlotPoints -> 100, PlotRange -> All]

It throws a warning:

NDSolve::ibcinc: Warning: boundary and initial conditions are inconsistent.

Looking for intuition as to what numerical issue makes this solution of NDSolve blow up unphysically

3 Answers3