How to integrate a symbolic sum?

Question

I'm trying to integrate a function that involves a finite sum:

$$\int_{-\infty}^{\infty}\sum_{j=1}^n (e^{-b t^2}r_j) \,dt$$

I think it should be possible to take the exponent outside the sum:

$$\int_{-\infty}^{\infty}\left(e^{-b t^2} \sum_{j=1}^n r_j \right)dt=\sum_{j=1}^n r_j \times \int_{-\infty}^{\infty}e^{-b t^2} dt$$

I write it in Mathematica like this:

$Assumptions=_\[Element]Reals
Assuming[
b>0,
Integrate[Sum[Exp[-b t^2]*r[j],{j,1,n}],{t,-\[Infinity],+\[Infinity]}]
]

This, however, simply returns the integral unchanged:

$$\int_{-\infty }^{\infty } \left(\sum _{j=1}^n e^{-b t^2} r(j)\right)\, dt$$

If I specify a number for $n$, I get the expected result:

$$\frac{\sqrt{\pi } (r(1)+r(2)+r(3)+r(4)+r(5))}{\sqrt{b}}$$

How do I extract $e^{-bt^2}$ outside the sum? Alternatively, how do I bring the integral inside the sum? More generally, how do I integrate this?

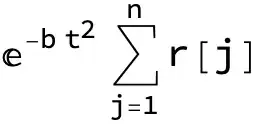
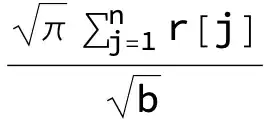
Why don't you move it outside yourself? Sum[r[j], {j, 1, n}]*Integrate[Exp[-b t^2], {t, -\[Infinity], +\[Infinity]}] — Domen, Jan 20 '22 at 16:36
@Domen, this is a simplified example. I actually have a bigger expression that'll get really long if I extract everything manually. I could probably integrate this by hand, but I was hoping that Mathematica can automate this for me. — ForceBru, Jan 20 '22 at 16:38
Simplify and FullSimplify also can't bring a constant factor outside the sum: FullSimplify[Sum[a*Indexed[r, j], {j, 1, n}]] returns the sum of a*r_j (as opposed. to a times the sum of r_j), but specifying a number instead of n correctly produces a*(r_1+r_2+...) — ForceBru, Jan 20 '22 at 16:45
I think the reason is that you can exchange sum and integrate if the sum is known to be finite. See when-can-a-sum-and-integral-be-interchanged and here Mathematica does not know the sum is finite of not, because it does not know r[j] is finite. For example, if you replace r[j] with just j then it works. ClearAll[b,n,j,r,t]; f[t_]:=Sum[Exp[-b t^2]*j,{j,1,n}]; Assuming[Element[b,Reals]&&b>0,Integrate[f[t],t]] and gives (n*(1 + n)*Sqrt[Pi]*Erf[Sqrt[b]*t])/(4*Sqrt[b]) ... — Nasser, Jan 20 '22 at 17:42
.. so if someone can figure how to tell Mathematica that the sum is finite or r[j] is finite, then may be there will be a better chance to have it work. — Nasser, Jan 20 '22 at 17:43
@Nesser, I tried adding assumptions like Indexed[r, j] > 0 && Indexed[r, j] < 1 to both the sum and the integral, but this didn't change anything. I also tried adding n > 0 && n < 6 to these assumptions to indicate that the sum is finite, but this didn't help either... — ForceBru, Jan 20 '22 at 17:58

Michael E2 · Answer 1 · 2022-01-21T06:13:16.533

Using linearExpand from How to do algebra on unevaluated integrals? :

Clear[linearExpand];
linearExpand[e_, x_, head_] := 
  e //. {op : head[arg_Plus, __] :> Distribute[op], 
    head[arg1_Times, rest__] :> 
     With[{dependencies = Internal`DependsOnQ[#, x] & /@ List @@ arg1}, 
      Pick[arg1, dependencies, False] head[
        Pick[arg1, dependencies, True], rest]]};
linearExpand[Sum[Exp[-b t^2]*r[j], {j, 1, n}], j, Sum]

Assuming[b > 0,
 Integrate[
  linearExpand[Sum[Exp[-b t^2]*r[j], {j, 1, n}], j, Sum],
  {t, -\[Infinity], +\[Infinity]}]
 ]

score 1 · Answer 2 · answered Jan 20 '22 at 18:21

Use a replacement Rule to swap the order when appropriate.

Clear["Global`*"]
swap = Integrate[Sum[f_, iter1_, opts1___], iter2_, opts2___] :> 
   Sum[Integrate[f, iter2, opts2], iter1, opts1];
expr[n_Integer?Positive] = Assuming[b > 0, (Integrate[
     Sum[Exp[-b t^2]*r[j], {j, 1, n}], {t, -∞, +∞}] /. swap)]
(* Sum[(Sqrt[Pi]r[j])/Sqrt[b], {j, 1, n}] )
expr[5] // Simplify
(* (Sqrt[π] (r[1] + r[2] + r[3] + r[4] + r[5]))/Sqrt[b] *)

How to integrate a symbolic sum?

2 Answers2

Linked