Plotting transformations of loci in a complex plane

Question

I found the solution to plot loci of complex numbers here, e.g. a locus of points of $z$ given $|z|=1$ is a circle centered at the origin with a radius 1.

But I am struggling to plot transformations, e.g. $T: w=2z$ would be an enlargement of the circle by a factor of 2.

I am trying something like this, but not very

ContourPlot[Evaluate[w /. w -> 2*z, z -> x + Iy, Abs[z] == 1],
{x, -4,4},
{y, -4, 4},
Axes -> True]

The argument to ContourPlot is not what you think. Look at it before to try to plot it. Evaluate[w /. w -> 2*z, z -> x + Iy, Abs[z] == 1] evaluates to Sequence[2 z, z -> Iy + x, Abs[z] == 1] Also note that Iy is a variable not a product, you need I y or I*y — Bob Hanlon, Jan 21 '22 at 14:13

Mathias · Answer 1 · 2022-01-21T14:13:50.093

3

So if you want to plot points that fulfill the equation |z| = w with w = 2. You can get the required result with

ContourPlot[Evaluate[Abs[z] == w /. { z -> x + I y, w -> 2}], {x, -3, 3}, {y, -3, 3}, Axes -> True]

edited Jan 21 '22 at 14:13

answered Jan 21 '22 at 14:05

Mathias

619
3
9

1

{y, 3, 3} should read {y, -3, 3} – Daniel Huber Jan 21 '22 at 14:10
Not really what I'm looking for. I am looking for syntax where $z$ is as defined, so I can play around with $w=f(z)$... i.e. a general solution, not specific to this example. – Mihail Jan 21 '22 at 14:20
You can use any equation in the contour plot you want. If you want to define a function f[z] you could use something like this: f[z_] := 3 (z - 1)^2; w = f[z] /. {z -> x + I y}; ContourPlot[Abs[w] == 1, {x, -3, 3}, {y, -3, 3}, Axes -> True] – Mathias Jan 21 '22 at 14:44
Still not what I am looking for. I need to be able to define $z$ as a condition for the locus instead of an equation. See the link in Q on how it was done for a plot w/o transformation. I need to extend that to a plot w/ transformation and be able to define the transformation separately. – Mihail Jan 21 '22 at 15:16

cvgmt · Answer 2 · 2022-01-22T00:16:30.563

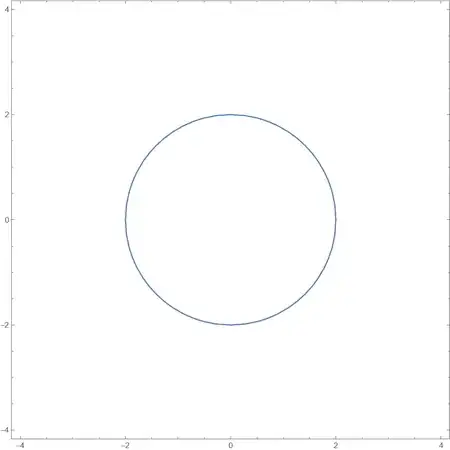
Since w=2z means that z=w/2,so we can plot Abs[w/2]==1

ComplexContourPlot[Abs[w/2] == 1, {w, -4 - 4 I, 4 + 4 I}]

Another example by using ComplexContourPlot.

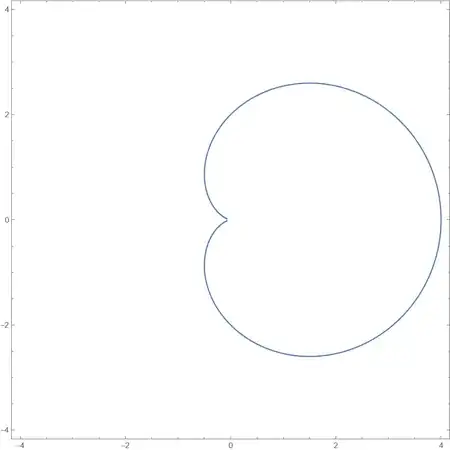
If you want to plot the mapping w=(z+1)^2 under the condition Abs[z]==1,we can solve z=Sqrt[w]-1 and plot Abs[Sqrt[w]-1]==1

ComplexContourPlot[Abs[Sqrt[w] - 1] == 1, {w, -4 - 4 I, 4 + 4 I}, 
 PlotPoints -> 50, MaxRecursion -> 4]

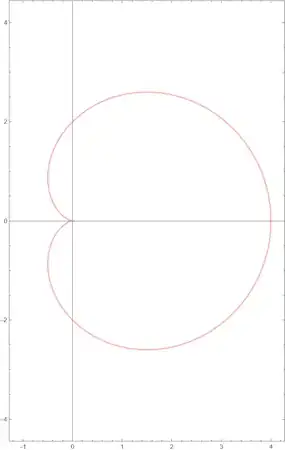
The same as ParametricRegion if we add the restricted condition Abs[z]==1.

reg = Block[{z = x + I*y}, 
   ParametricRegion[{ReIm[(z + 1)^2], Abs[z] == 1}, {x, y}]];
Region[reg, Axes -> True, AspectRatio -> Automatic, 
 BaseStyle -> Thick]

If we rewrite Abs[z]==1 by z=Exp[I*t],0<=t<=2 π, then ParametricPlot also work.

Block[{z = Exp[I*t]}, 
 ParametricPlot[ReIm[(z + 1)^2], {t, 0, 2 π}]]

Set MeshFunctions -> {Norm[{#3, #4}] &}, Mesh -> {{1}} also means that Abs[z]==1.

Block[{z = x + I*y}, 
 ParametricPlot[ReIm[(z + 1)^2], {x, -1, 1}, {y, -1, 1}, 
  MeshFunctions -> {Norm[{#3, #4}] &}, Mesh -> {{1}}, 
  MeshStyle -> {Thick, Red}, PlotStyle -> None, BoundaryStyle -> None,
   PlotPoints -> 50]]

Abs[z]==1 is the boundary of Disk[], we can use ParametricPlot again.

Block[{z = x + I*y}, 
 ParametricPlot[ReIm[(z + 1)^2], {x, y} ∈ Disk[], 
  BoundaryStyle -> Red, PlotStyle -> None, PlotPoints -> 50]]

Plotting transformations of loci in a complex plane

2 Answers2