How to tell when a job is too big for the pattern matcher?

Question

Pattern matching is great but it has its limitations. Consider sorting a list of numbers from smallest to largest:

RandomSample[Range[10]] //. {a___, b_, c_, d___} /; b > c :> {a, c, b, d}

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

However, running

RandomSample[Range[1000]] //. {a___, b_, c_, d___} /; b > c :> {a, c, b, d}

ReplaceRepeated::rrlim: Exiting after {<<1000>>} scaned 65536 times. >>
{1, 2, 3, 4, 5, 6, 7, 9, 11, 13, <<990>>}

is a different story. The code takes a long time to run and the resulting output is not sorted properly.

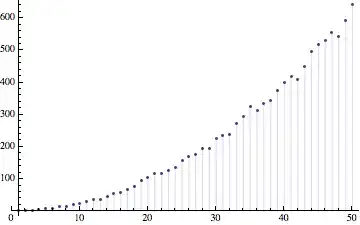
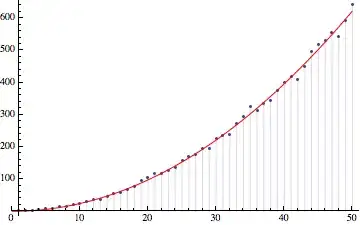
Now, obviously, we would want to use Sort in this type of scenario, but now I'm curious to know: at what point does a job become too computationally intensive for the pattern matcher?

Good question--I hadn't appreciated this limitation before. BTW, if you use indentation rather than backticks, your code will be syntax-highlighted in addition to being placed in a code block. See my edits to your post if you're unclear how to do this. — Oleksandr R., Jun 02 '13 at 04:46
Actually, on running your code, I see the message (ReplaceRepeated::rrlim), which you don't mention in your question, notes that this is a limitation of ReplaceRepeated, rather than the pattern matcher. You can change the threshold using the MaxIterations option. As far as I know, if you use pure pattern matching, there is no in-principle limitation except that dictated by the scaling behavior of the pattern you are matching. (In this case, the asymptotics are very poor, so that it takes a lot longer on a longer list is no surprise.) — Oleksandr R., Jun 02 '13 at 04:52
I see. Would I use Block if I wanted to locally change MaxIterations? — John Smith, Jun 02 '13 at 04:55
MaxIterations is an option name, not a Symbol with an assigned value, so I do not believe that method will work. You will need to use SetOptions or provide the option in ReplaceRepeated[. . ., options]. — Mr.Wizard, Jun 02 '13 at 04:57
Closely related: http://mathematica.stackexchange.com/q/237/121 — Mr.Wizard, Jun 02 '13 at 04:58
This is an option for ReplaceRepeated, rather than a global value like $IterationLimit. You have to write the ReplaceRepeated call out in full rather than using its sigil (//.). So, for example: ReplaceRepeated[RandomSample[Range[1000]], {a___, b_, c_, d___} /; b > c :> {a, c, b, d}, MaxIterations -> Infinity]. But, in general, one should beware of patterns such as this, because pathological scaling is all too easy to encounter. — Oleksandr R., Jun 02 '13 at 04:59
@Oleksandr I don't recall seeing that particular bit of programming jargon before. Your usage doesn't quite match Wikipedia's; is that intentional? To your knowledge is this term used by other Mathematica programmers? — Mr.Wizard, Jun 02 '13 at 06:39
@Mr.Wizard I thought this was common usage in the Mathematica community. Even if not, I certainly didn't invent it, but I don't remember where I saw it first. Though the meaning differs from other languages, since the "ordinary" usage isn't really applicable here, it seems like a perfectly good coinage to me. — Oleksandr R., Jun 02 '13 at 16:50

rm -rf · Answer 1 · 2013-06-02T06:06:20.123

Rather than it being "too big" for the pattern matcher, the problem here is because of the use of //. which applies the rule repeatedly till the result no longer changes (i.e. the list is sorted). In other words, the issue is that of the complexity of the algorithm you're using (//. with ___) rather than the programming paradigm that you've chosen (pattern matching). If you implemented the same algorithm in a procedural style, you'll experience the same degree of "slowness".

You can perform a simple test to see how your algorithm scales:

ClearAll@iters
iters[n_Integer] := iters[n] = 
    Table[FixedPointList[
            ReplaceAll[#, {a___, b_, c_, d___} /; b > c :> {a, c, b, d}] &, 
            RandomSample[Range[n]]
        ] // Length, 
        {10}] // Mean // N

plot = DiscretePlot[iters[n], {n, 50}]

This looks like $\mathcal{O}(n^2)$, which you can confirm with

fit = FindFit[iters /@ Range@50, c x^n, {c, n}, x]
(* {c -> 0.227266, n -> 2.02332} *)

plot ~Show~ Plot[c x^n /. fit, {x, 0, 50}, PlotStyle -> Red]

So it is not surprising that for $n=1000$, you are performing ~ 267,000 replacements, which is the primary reason for your slowness.

As Oleksandr has pointed out, you can modify MaxIterations to remove the soft limit of 65536 iterations, but I'd strongly advise against making a habit of it, and instead urge you to investigate the specific pattern/choice of algorithm used.

R.M, I voted for this answer, but given that Leonid addressed this specific sorting method in his answer to the question I linked, do you think it would be better to have this information there, and close this as already answered? — Mr.Wizard, Jun 02 '13 at 06:43
I just realised that you did something different to what I thought you had done on a first reading. Although the number of iterations is quadratic in the list length, matching the pattern depends linearly on that length by itself. So, the total time complexity is cubic, not quadratic. This difference is quite often what distinguishes between a reasonable algorithm and an impractical one, so I think it's important to be clear on this point. — Oleksandr R., Jun 02 '13 at 17:09

How to tell when a job is too big for the pattern matcher?

1 Answers1