Plot[{1/(3 x*Sqrt[1 - x^2]), 1/(3 x*Sqrt[1 - x^2])}, {x, 0, 1},
PlotStyle -> Directive[AbsoluteThickness[2], Opacity[1], Black],
PlotRange -> {0, 1},
GridLines -> {{0.35, 0.94}, {}},
Method -> "GridLinesInFront" -> True,
GridLinesStyle -> Directive[Black, Dashed],
Filling -> {1 -> {Bottom, GrayLevel[.8]}, 2 -> {Top, GrayLevel[.6]}},
RegionFunction -> (.35 <= # <= .94 &)]
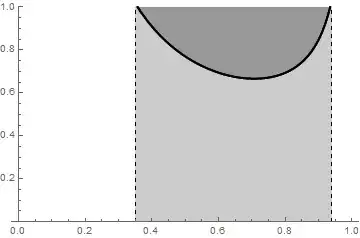
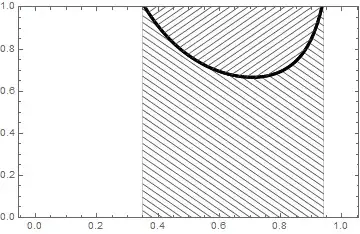
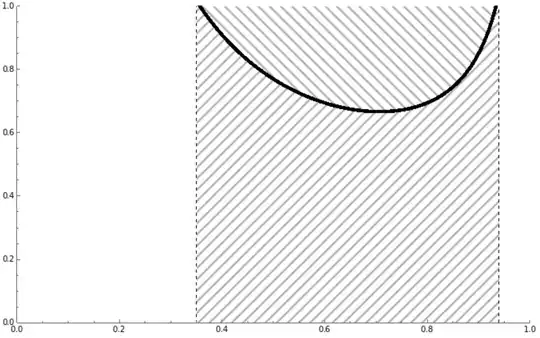
To get hatched-filling in older versions we can use ParametricPlot with the options MeshFunctions + Mesh + MeshStyle:
Show @ MapThread[
ParametricPlot[{x, # t + (1 - t) 1/(3 x*Sqrt[1 - x^2])},
{x, 0.35, 0.94}, {t, 0, 1},
PlotRange -> {0, 1},
ImageSize -> Medium,
AspectRatio -> 1/GoldenRatio,
GridLines -> {{0.35, 0.94}, {}},
BoundaryStyle -> None,
PlotStyle -> None,
MeshStyle -> Directive[GrayLevel[.3], Opacity[1],
AbsoluteThickness[1], CapForm["Butt"]],
MeshFunctions -> {#4 &, #2},
Mesh -> {{{0, Directive[Black, Opacity[1], AbsoluteThickness[3],
CapForm["Butt"]]}}, #3}] &,
{{0, 1}, {# + #2 &, # - #2 &}, {50, 25}}]
$Version
"11.3.0 for Microsoft Windows (64-bit) (March 7, 2018)"
See also:
- Generating hatched filling using Region functionality
- Texture or shading to avoid requiring color printing




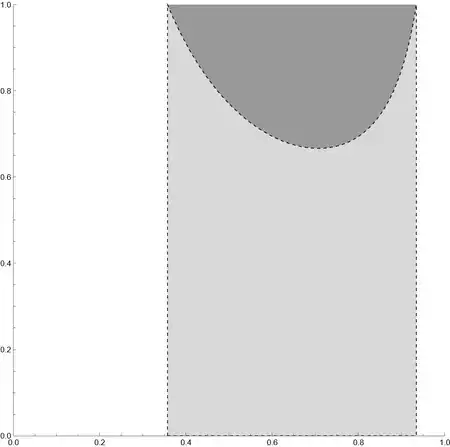
Filling! – Ulrich Neumann Jan 28 '22 at 12:10