I have solved a differential equation by using NDSolve with xmax=3
ydum = x/L[t];
expr1 = Expand[(1/c^2)*D[\[Psi][ydum, t], {t, 2}] -
D[\[Psi][ydum, t], {x, 2}] + ((m^2*c^2)/h^2)*\[Psi][ydum,
t] /. \[Psi][ydum, t] -> \[Psi][y, t] /. x -> y*L[t]]
m = 1;
c = 1;
h = 1;
\[Omega] = 1;
L[t_] := 2 + Sin[\[Omega]*t];
sol = NDSolve[{expr1 == 0, [Psi][0, t] == 0, [Psi][1, t] ==
0, [Psi][y, 0] ==
Sqrt[2 (m c)/(c Sqrt[m^2 c^2 + [Pi]^2 h^2/L[0]^2] L[0])]
Sin[ [Pi] y]}, [Psi], {y, 0, 1}, {t, 0, 3}]
Then I plot this with Plot3D
Plot3D[Abs[Evaluate[\[Psi][y, t] /. sol]], {y, 0, 1}, {t, 0, 10},
AxesLabel -> {y, t, \[Psi]}]
Then I changed the xmax of my NDSolve to 10 and plot the answer still with t ranging from 0 to 3
sol = NDSolve[{expr1 == 0, \[Psi][0, t] == 0, \[Psi][1, t] ==
0, \[Psi][y, 0] ==
Sqrt[2 (m c)/(c Sqrt[m^2 c^2 + \[Pi]^2 h^2/L[0]^2] L[0])]
Sin[ \[Pi] y]}, \[Psi], {y, 0, 1}, {t, 0, 10}]
The 2 graphs are clearly different. From my understanding, changing the range in which a differential equation is evaluated shouldn't change the answer (I have also tried it with simpler differential equation and this didn't happen). Can someone explain why this is happening?
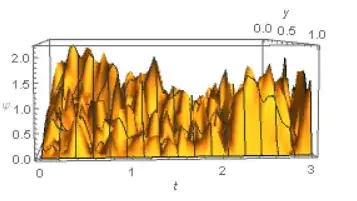
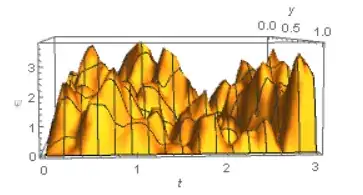
xmaxin the code? – Alex Trounev Feb 08 '22 at 12:24xmax=10in my first equation, but the plot belongs toxmax=3though. – ForacleFunacle Feb 08 '22 at 14:29