The first part of this solution derives from my previous post Fill in the StringBlank.
Define a utility function called unblankify.
Clear[unblankify]
unblankify[w_String, m_String : "_"] := Module[{pattern, s2},
s2 = StringSplit[w, m -> Blank[]];
pattern = StringExpression @@ s2;
DeleteDuplicates@ToLowerCase@DictionaryLookup[pattern]
]
It is not necessary to use DeleteDuplicates or ToLowerCase in this definition, but that does get rid of some proper nouns and acronyms spelled with upper case letters etc.
Usage. If there is a letter marked with a green background on the game board, then one can use this fact to limit possibilities. For example:
unblankify["ar___"]
{"arbor", "arced", "ardor", "areal", "areas", "arena", "argon",
"argot", "argue", "arias", "arise", "armed", "armor", "aroma",
"arose", "arras", "array", "arrow", "arsed", "arson", "artsy",
"arums"}
Next, I investigated how many 5-letter words constitute the starting set.
words5 = unblankify["_____"];
Length@words5
6529
and the count of characters in the entire set in order to arrive at good initial word guesses.
charsFreq = Flatten@(Characters /@ words5) // Counts // Sort
<|"ü" -> 1, "ö" -> 1, "è" -> 1, "ñ" -> 1, "ô" -> 1, "à" -> 1, "ó" ->
2, "ê" -> 2, "-" -> 2, "é" -> 13, "'" -> 27, "q" -> 56, "j" -> 140,
"x" -> 140, "z" -> 170, "v" -> 377, "w" -> 534, "f" -> 561, "k" ->
650, "g" -> 756, "b" -> 814, "h" -> 908, "m" -> 963, "p" -> 966, "y"
-> 968, "c" -> 1081, "u" -> 1178, "d" -> 1338, "n" -> 1617, "t" -> 1711, "l" -> 1854, "i" -> 1902, "o" -> 2087, "r" -> 2165, "a" ->
2962, "s" -> 3242, "e" -> 3453|>
If converted to frequencies, these would be closely related to the frequencies of standard 26 characters in the entire dictionary but the numbers will not be the same.
The most used letters can be turned into 5-letter words such as "arose", "until". Notice that these two words contain all the vowels, so a litmus test would be to remove any words that don't have any of these letters and reach an empty set.
After reducing possibilities using the unblankify function, it is time to remove words that contain letters marked in black (that are not present in the answer) and include letters that are shown in amber (that are present but not at their correct location yet). Below, I am using the "aroseuntil" as example characters that should not be present from the entire words5 set.
Pick[unblankify["_____"], (ContainsAll[Characters@""]
[Characters@#] &&
ContainsNone[Characters@"aroseuntil"]
[Characters@#]) & /@ unblankify["_____"]
]
{"pygmy", "why'd"}
Playing
First step: Here "u" is the only vowel after two attempts and characters from the string "arosentil" should be discarded for future guesses.
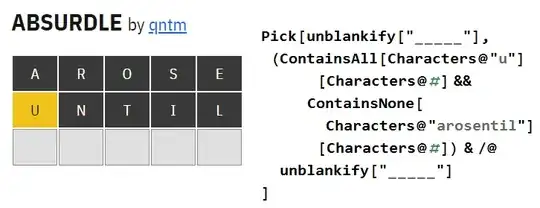
The choices reduce to:
{"buddy", "buffy", "buggy", "bumph", "bumpy", "chuck", "chuff", \
"chump", "duchy", "ducky", "duffy", "dummy", "dumpy", "fuggy", \
"fuzzy", "gummy", "guppy", "hubby", "huffy", "humph", "jumpy", \
"khufu", "kudzu", "mucky", "muddy", "muggy", "mummy", "muzzy", \
"pudgy", "puffy", "puppy", "yucky", "yukky", "yummy"}
Second step: I entered the word "duchy" as there is no point in entering words with two similar letters and it fixes the "u" and "y", so these were added to the unblankify portion and the characters from "dch" were added to exclusions.

Now the possibilities are:
{"buffy", "buggy", "bumpy", "fuggy", "fuzzy", "gummy", "guppy",
"jumpy", "muggy", "mummy", "muzzy", "puffy", "puppy", "yukky",
"yummy"}
Try it and it will systematically not let you get to the final answer except through the hardest path. Seven is a common number of attempts before the game engine runs out of possibilities. If the answer is fixed from the start (as in Wordle), then four attempts are often sufficient.

