Using the collocation method proposed here, recently this problem has been solved. I am trying to solve a similar problem described by the equations given below. My attempt in Mathematica is following.
$T$ is in the domain $x\in[0,1], y\in[0,1]$
eq1 = \[Lambda]x D[T[x, y], x, x] + \[Lambda]y D[T[x, y], y, y] ==
0; bc1 = {(D[T[x, y], y] + rh (Tfh[x] - T[x, y]) == 0) /.
y -> 1, (D[T[x, y], y] + rc (T[x, y] - Tfc[x]) == 0) /.
y -> 0}; eq2 = D[T[x], x] + bh (Tfh[x] - T[x]) == 0;
bc2 = Tfh[0] == 1;
eq3 = D[Tfc[x], x] + bc (T[x] - Tfc[x]) == 0;
bc3 = Tfc[0] == 0;
UE[m_, t_] := Cos[m t] Exp[-m t]
nn = 3;
dx = 1/(nn); xl = Table[l*dx, {l, 0, nn}]; ycol =
xcol = Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, nn + 1}]; Psijk =
Table[UE[n, t1], {n, 0, nn - 1}]; Int1 = Integrate[Psijk, t1];
Int2 = Integrate[Int1, t1];
Psi[y_] := Psijk /. t1 -> y;
int1[y_] := Int1 /. t1 -> y;
int2[y_] := Int2 /. t1 -> y; M = nn;
M = nn; U1 = Array[a1, {M, M}]; U2 = Array[a2, {M, M}]; G1 =
Array[g1, {M}]; G2 = Array[g2, {M}]; G4 = Array[g4, {M}]; G5 =
Array[g5, {M}];
Tfhx[x_] := (Psi[x].G5);
Tfcy[x_] := (Psi[x].G4);
Tfh[x_] := (int1[x].G5);
Tfc[x_] := (int2[x].G4);
u1[x_, y_] := (int2[x].U1.Psi[y]) + x Psi[y].G1;
u2[x_, y_] := (Psi[x].U2.int2[y]) + y Psi[x].G2;
uy[x_, y_] := (Psi[x].U2.int1[y]) + Psi[x].G2;
ux[x_, y_] := (int1[x].U1.Psi[y]) + Psi[y].G1;
uxx[x_, y_] := (Psi[x].U1.Psi[y]);
uyy[x_, y_] := (Psi[x].U2.Psi[y]);
[Lambda]x = 1/0.025^2; [Lambda]y = 1/0.002^2; bh = 0.625; bc =
4 bh; rh = 3000 0.002/390; rc = 3000 0.002/390;
eqn = Join[
Flatten[Table[([Lambda]x uxx[xcol[[i]],
ycol[[j]]] + [Lambda]y uyy[xcol[[i]], ycol[[j]]]) == 0, {i,
M}, {j, M}]],
Flatten[Table[
u1[xcol[[i]], ycol[[j]]] - u2[xcol[[i]], ycol[[j]]] == 0, {i,
M}, {j, M}]], Flatten[Table[ux[1, ycol[[i]]] == 0, {i, M}]],
Flatten[Table[uy[xcol[[i]], 1] == 0, {i, M}]],
Flatten[Table[ux[0, ycol[[i]]] == 0, {i, M}]],
Flatten[Table[uy[xcol[[i]], 0] == 0, {i, M}]],
Flatten[Table[
uy[xcol[[i]], 1] + rh (Tfh[xcol[[i]]] - u2[xcol[[i]], 1]) ==
0, {i, M}]],
Flatten[Table[
uy[xcol[[i]], 0] + rc (u2[xcol[[i]], 0] - Tfc[xcol[[i]]]) ==
0, {i, M}]],
Flatten[Table[
Tfhx[xcol[[i]]] + bh (Tfh[xcol[[i]]] - u2[xcol[[i]], 1]) ==
0, {i, M}]],
Flatten[Table[
tcy[xcol[[i]]] + bc (u2[xcol[[i]], 0] - Tfc[xcol[[i]]]) == 0, {i,
M}]], Table[Tfh[xcol[[i]]] == 1., {i, M}],
Table[Tfc[xcol[[i]], 0] == 0., {i, M}]];
var = Join[Flatten[U1], Flatten[U2], Flatten[G1], Flatten[G2],
Flatten[G4], Flatten[G5]];
{v, mat} = CoefficientArrays[eqn, var];
sol = LinearSolve[mat, -v];
rule = Table[var[[i]] -> sol[[i]], {i, Length[var]}];
{Plot[Evaluate[Tfc[x] /. rule], {x, 0, 1}, ColorFunction -> "Rainbow",
MeshStyle -> White, PlotLegends -> Automatic, PlotLabel -> Tfc],
Plot3D[Evaluate[Tfh[x] /. rule], {x, 0, 1},
ColorFunction -> "Rainbow", MeshStyle -> White,
PlotLegends -> Automatic, PlotLabel -> Tfh],
Table[Plot3D[Evaluate[u1[x, y] /. rule], {x, 0, 1}, {y, 0, 1},
ColorFunction -> "Rainbow", MeshStyle -> White,
PlotLegends -> Automatic, PlotLabel -> T[y]], {y, 0, 1, .5}]}
The code above tries to solve the following equations:
$$\lambda_x \frac{\partial^2 T}{\partial x^2}+\lambda_y \frac{\partial^2 T}{\partial y^2}=0 \tag1$$
Zero gradient of $T$ at $x=0,1$.
At $y=0,1$ the solid ($T$) is exposed to two different fluids following opposite to each other (separated by the solid).
$$\frac{\partial T(x,0)}{\partial y}+r_c(T(x,0)-t_c)=0\tag2$$ $$\frac{\partial T(x,1)}{\partial y}+r_h(t_h-T(x,1))=0\tag3$$
The fluid temperatures $t_h,t_c$ are governed by:
$$\frac{\partial t_h}{\partial x}+\beta_h(t_h-T)=0\tag4$$ $$\frac{\partial t_c}{\partial x}+\beta_c(T-t_c)=0\tag5$$
A reduced order model
The above problem can be simplified if one averages the solid temperature along the $y$ direction to get the following solid governing equation instead of $(1)$:
$$\kappa \frac{\mathrm{d}^2 T}{\mathrm{d} x^2} + \mu b_h(t_h-T) - \nu b_c(T-t_c)=0 \tag6$$
with $T'(0)=T'(1)=0$. Equation $(6)$ is still coupled with Equation $(4)$ and Equation $(5)$. Some parameter values are bc=12.38, bh=25.32, mu=1.143, nu=1, kappa=2.16
Some cases behaving wierdly
Although the wavelet method works really fine, but I am facing problems with some particular set of flow configurations, which are physically important. One of them being the following:
λx = 1/0.025^2; λy = 1/0.001^2; bh = 173.6539; bc = 355.1724; rh = 134.31 0.001/16; rc = 305.2252 0.001/16;
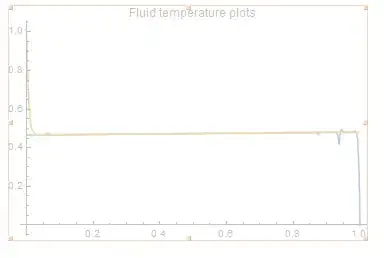
Upon executing these parameters, with the wavelet method such that nn=16, I obtain the following plots of the fluid temperature profiles
For nn=40, the plot is like the following:
Lastly, the nn=96 gives:
As it is clear that the fluid temperature profiles experience spikes. Although, they do decrease in magnitude with increasing nn. I would like to know the reason as to why this is happening and if they can be removed. I have checked that the insulation boundary conditions on x=0,1 are satisfied to the order of 10^-12.




eq2 = D[T[x], x] + bh (Tfh[x] - T[x]) == 0;. – Alex Trounev Feb 13 '22 at 03:00y=0, y=1are opposite then it should beeq2 = D[Tfh[x], x] + bh (Tfh[x] - T[x, 1]) == 0; bc2 = Tfh[0] == 1; eq3 = D[Tfc[x], x] + bc (T[x, 0] - Tfc[x]) == 0; bc3 = Tfc[1] == 0;– Alex Trounev Feb 13 '22 at 03:32eqn, I have usedbh (Tfh[xcol[[i]]] - u2[xcol[[i]], 1])and similarly for the bc equation. – Avrana Feb 13 '22 at 04:04eqnin the linetcy[xcol[[i]]] + bc (u2[xcol[[i]], 0] - Tfc[xcol[[i]]]) == 0.tcyis not defined. – Alex Trounev Feb 13 '22 at 04:53Tfc? In your code there isbc3 = Tfc[0] == 0;, but I have used oppositebc3 = Tfc[1] == 0;. – Alex Trounev Feb 13 '22 at 15:27UE[m_, t_] := Cos[m t] Exp[-m t]. I just removed the parts relating to Euler wavelets. So, thebc3=Tfc[1]==0is the boundary condition I used to report the results I mentioned in the comments to your answer. – Avrana Feb 13 '22 at 15:45bc, bh. To avoid this instability we need takedx<Min[{1/bc,1/bh}], andnn=Round[1/dx ] consequently. Therefore,nn>355for this case. So, we need supercomputer or other method to compute cases with largebc, bh`. – Alex Trounev Feb 15 '22 at 16:28