How do I find the coordinates of points in this image?

Question

I have never used image processing with Mathematica. I need to get the coordinates of the red points from this image I made in Illustrator. Is there a way to get Mathematica to read or detect the x-y coordinates?

enter image description here

Of course, you need a coordinate system... where is the origin, for instance? — J. M.'s missing motivation, Jun 04 '13 at 05:54
Anywhere can be the origin. I will shift and scale the numbers as need be! — QuantumDot, Jun 04 '13 at 06:15
Perhaps this question and its answers can be of help for you. I guess with a bit of work you can create a solution for your problem. — partial81, Jun 04 '13 at 06:15
After applying Binarize[] to the OP's image, the question is now equivalent to the one linked by @partial81; unless I see a reason why this is not a dupe, I'm leaning towards closing this. — J. M.'s missing motivation, Jun 04 '13 at 06:36
Wouldn't PixelValuePositions[i, Red, .2] be quicker though? — cormullion, Jun 04 '13 at 06:47
I agree @0x4A4D. If QuantumDot cannot tell us why his question needs another solution, I would close it too. — partial81, Jun 04 '13 at 06:52
No, really; why are people not posting answers to the other question that was previously linked? — J. M.'s missing motivation, Jun 04 '13 at 19:33
Quick question: if it's made in Illustrator, can't you export to EPS and extract the points using string processing? Does it have to be done with image techniques? — Jens, Jun 04 '13 at 23:56
@Jens I was hoping to figure out how to do that -- but I couldn't, so doing it this way was my last-ditch try. — QuantumDot, Jun 05 '13 at 05:41
whether it is possible in the same way to get the coordinates of points on the curve? — Alex Kulay, Apr 14 '14 at 12:52
This is not Mathematica, but I prefer PlotDigitizer.com. It is a GUI solution and can extract data from several types of graphs, including XY. You check out its free online app. — Anonymous, Jan 15 '21 at 10:30

score 24 · Accepted Answer · answered Jun 04 '13 at 07:47

24

A solution for Mathematica version 9:

image = Import["https://i.stack.imgur.com/R0Dqo.png"]
pts = PixelValuePositions[image, Red, .2];
ListPlot[pts, 
 PlotStyle -> Darker@Orange, 
 PlotMarkers -> {Automatic, .05}, 
 PlotRange -> {{0, 1500}, {0, 800}}, 
 ImageSize -> 600]

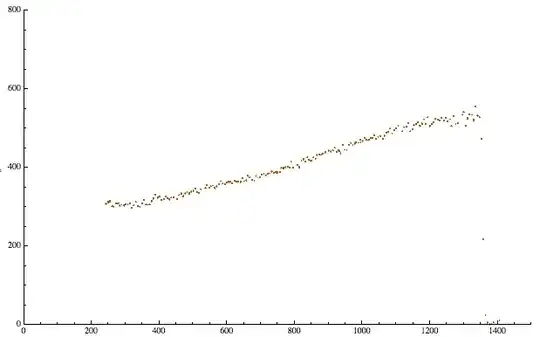
listplot of points

answered Jun 04 '13 at 07:47

cormullion

24,243
4
64
133

1

Very nice solution! Fortunately the question was not closed ;-) I did not know the PixelValuePositions so far (seems to be new in MMA 9). – partial81 Jun 04 '13 at 08:11
Are there really two thousand points in the original image (length of pts above)? – BoLe Jun 04 '13 at 09:35
PixelValuePositions[Thinning@ColorNegate@ImageCrop@Binarize@image, 1] perhaps. – BoLe Jun 04 '13 at 09:37
Or thinned = DeleteDuplicates[pts, EuclideanDistance[#1, #2] < 2 &] to keep it as data...? – cormullion Jun 04 '13 at 10:33
@cormullion I agree, should distance 2 not exclude certain original dot. – BoLe Jun 04 '13 at 12:03
I already gave a +1, but PixelValuePositions proved useful, elsewhere. – rcollyer Jun 04 '13 at 19:53
I get a nice clustering using this: pts = Mean /@ Gather[pts, EuclideanDistance[#1, #2] < 4 &]; – Murta Jun 05 '13 at 01:29

score 8 · Answer 2 · edited Jun 16 '20 at 09:23

The question leaves open what a "point" is, as opposed to a pixel.

Attempt at points

If points overlap in the image, it is beyond my skill to separate them. Others here have far more experience in image processing and may be able to suggest things, within limits. If the points are separated, then here's a rough stab at finding them:

MorphologicalComponents[Binarize[img, {0.29, 0.6}], 0.68] // Colorize

MorphologicalComponents

(rules = ArrayRules[MorphologicalComponents[Binarize[img, {0.29, 0.6}], 0.68]];
  points = Mean /@ Map[First, GatherBy[rules, Last], {2}];) // Timing
Length[points]

{0.072981, Null}
195

The points are image coordinates; we should convert them to graphics coordinates before plotting:

ListPlot[{#[[2]], Last@ImageDimensions[img] - #[[1]]} & /@ points, 
 PlotMarkers -> {Automatic, 2}, 
 PlotRange -> Transpose[{{0, 0}, ImageDimensions[img]}], 
 PlotRangePadding -> 50, AxesOrigin -> {0, -50}]

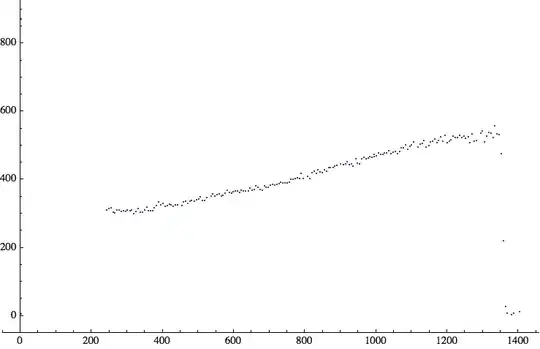
Point plot

Pixels

The same method is an efficient way to get the pixels (especially if you do not have v9 and PixelValuePositions to use).

(rules = ArrayRules[MorphologicalComponents[Binarize[img, {0.29, 0.6}], 0.68]];
  pixelCoords = SparseArray[rules]["NonzeroPositions"];) // Timing
Length@pixelCoords

{0.070562, Null}
2629

ListPlot[{#[[2]], Last@ImageDimensions[img] - #[[1]]} & /@ pixelCoords,
 PlotMarkers -> {Automatic, 0.25}, 
 PlotRange -> Transpose[{{0, 0}, ImageDimensions[img]}], 
 PlotRangePadding -> 50, AxesOrigin -> {0, -50}]

Pixel plot

This way is nearly as fast and gives the same result as above:

pixelCoords = Position[ImageData@Binarize[img, {0.29, 0.6}], 1]; // Timing
Length@pixelCoords

{0.108690, Null}
2629

Good work, +1. Although we're probably all just exploring for fun, since the OP's Illustrator file likely contains the actual coordinate pairs of every point — cormullion, Jun 04 '13 at 19:39
@cormullion Yes, processing images is an attractive pastime, but it's not something I am very good at yet. — Michael E2, Jun 04 '13 at 23:40

score 4 · Answer 3 · edited Dec 17 '23 at 12:00

4

Using relatively simple functions:

c = Import["https://i.stack.imgur.com/R0Dqo.png"] ;
a = Rasterize[c];
reds = Cases[Union[Flatten[a[[1, 1]], 1]], {r_ /; r > 200, g_ /; g < 50, b_ /; b < 50}];
Row[{First[Timing[b = Map[Position[a[[1, 1]], #] &, reds]]], " seconds"}]

13.073 seconds

ListPlot[Reverse /@ Flatten[b, 1], PlotStyle -> Red, AxesOrigin -> {0, 0}]

enter image description here

edited Dec 17 '23 at 12:00

azerbajdzan

15,863
1
16
48

answered Jun 04 '13 at 14:13

Chris Degnen

30,927
2
54
108

score 3 · Answer 4 · answered Jun 04 '13 at 16:05

3

Another way without Mathematica version 9 PixelValuePositions

img = Import["https://i.stack.imgur.com/R0Dqo.png"];
pix = Round[ImageData[img, DataReversed -> True]];
ListPlot[Reverse /@ Position[pix, {1, 0, 0}], AxesOrigin -> {0, 0}]

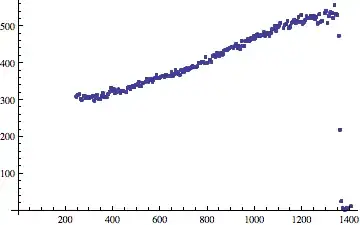
enter image description here

answered Jun 04 '13 at 16:05

dstahr

381
1
3
8

How do I find the coordinates of points in this image?

4 Answers4

Attempt at points

Pixels

Linked