This is because of your external force:
(Quantity[
-0.5 Normalize[QuantityMagnitude[#["Velocity"]]](*An extra damping*)
, "Newtons"] &)
blowing up at small velocity, because of the normalizing factor going infinity $$\hat{v}=\left(\frac{1}{\sqrt{v\cdot v}}\right)v\;,\quad \lim_{v\to\vec{0}}\frac{1}{\sqrt{v\cdot v}}=\infty\;.$$
To avoid this, you could define the external force as a piecewise function:
(Piecewise[{
{Quantity[-0.5 Normalize[QuantityMagnitude[#["Velocity"]]], "Newtons"], Norm[QuantityMagnitude[#["Velocity"]]] > 10^-1},
{0, Norm[QuantityMagnitude[#["Velocity"]]] <= 10^-1}
}] &)
As a side note, specifying the units and mapping the quantities to their magnitude is not very necessary but has a significant performance impact. Compare, for example, with this:
n = 4;
countTime = 5;
SeedRandom[5];
initPos = SetPrecision[RandomPoint[Disk[], n], 10];
data = NBodySimulation[
Association[
"PairwisePotential" -> "Coulomb",
"Region" -> Disk[],
"ExternalForce" -> (Piecewise[{
{-0.5 Normalize[#["Velocity"]], Norm[#["Velocity"]] > 10^-1},
{0, Norm[#["Velocity"]] <= 10^-1}
}] &)
],
Association[
"Mass" -> 1,
"Position" -> #,
"Velocity" -> {0, 0},
"Charge" -> 10^-5
]& /@ initPos
, countTime];
colors = RandomColor[n];
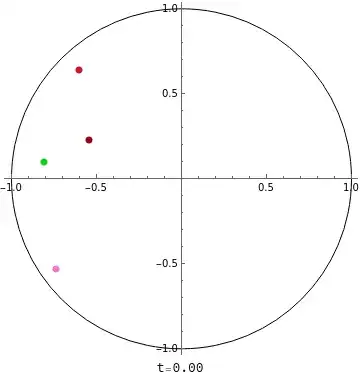
Manipulate[
Graphics[
{Circle[], Red, PointSize[0.02], Riffle[colors, Point /@ data[All, "Position", time]]}
, Axes -> True]
, {time, $MachineEpsilon, countTime, Appearance -> "Labeled"}]
Addendum. This is an explicit explanation as to why the Normalize part blows up in NDSolve. User @xzczd insists otherwise, further claiming that Normalize doesn't transform into anything, such as x/Abs[x]. While that's partially true, it's only when the input is already given as a number. When NDSolve computes a step, it first turns the terms containing variables/target function in the equation into their effective numerical form as much as possible, such as Normalize[{x'[t],y'[t]}] to {x'[t]/Norm[{x'[t],y'[t]}],y'[t]/Norm[{x'[t],y'[t]}]} and then to {x'[t]/Sqrt[Abs[x'[t]^2+y'[t]^2]],y'[t]/Sqrt[Abs[x'[t]^2+y'[t]^2]]}. One can easily check this:
Trace[NDSolve[{Normalize[{f[t], 0}] == {f'[t], 0}, f[0] == 1}, f, {t, 0, 1}]][[1, 1, 1]]
(* {Normalize[{f[t], 0}], {f[t]/Abs[f[t]], 0}} *)
Now, in the case of damping, if "Velocity" or numerical f'[t] gets small at some sufficiently large step (sufficient enough to kill off the precision) during NDSolve, then it's straightforward f'[t]/Abs[f'[t]] blows up:
q1 = 1`10;
q2 = 1`10 + 1/5*10^-9;
dq = q2 - q1;
Precision /@ {q1, q2, dq}
(* {10., 10., 0.} *)
dq/Norm[dq]
(* Error encountered; Indeterminate *)
One workaround is to define the function (damper) piecewise, for small Norm. This is precisely what I did above, which effectively solved the problem.

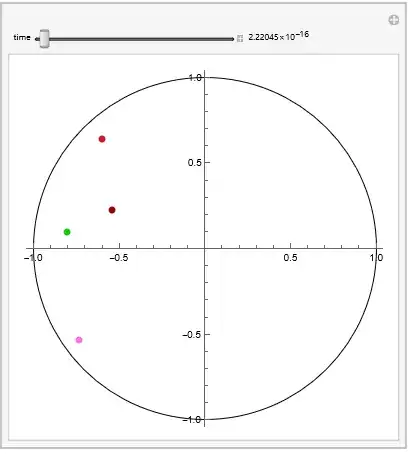
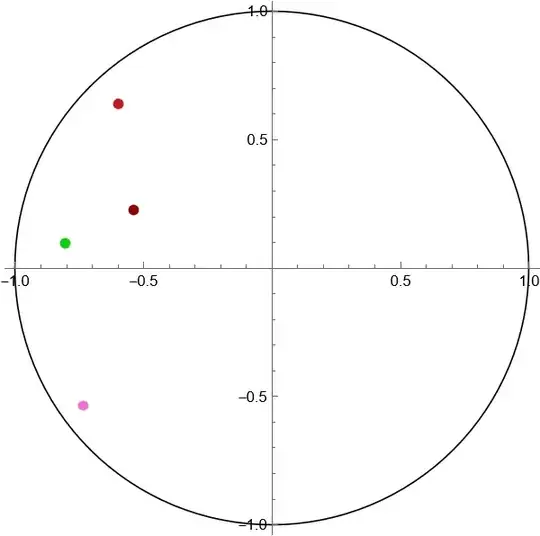


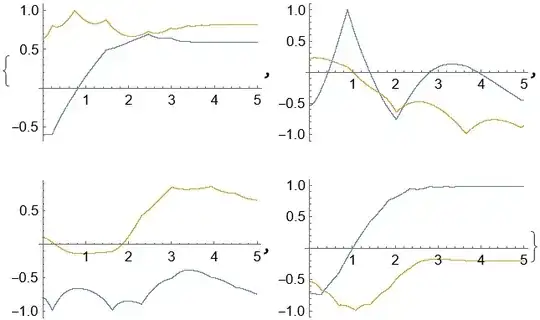

NDSolveby providing the optionMethod. Because the systems are Hamiltonian, the default choice inNBodySimulationis"SymplecticPartitionedRungeKutta". You can try withMethod -> "StiffnessSwitching"which goes past the stiffness point, but soon after that, unfortunately, the balls wander outside the circle ... Internally, reflections from the walls are performed viaWhenEvents. Perhaps there is already an answer here at MMA.SE on how to properly set upWhenEvents for such cases ... – Domen Feb 24 '22 at 19:50ExplicitMidpoint,StiffnessSwitchingandExtrapolationall will avoid error result the balls wander outside the circle. I don't know if this is a bug or not inNBodySimulation– yode Feb 24 '22 at 20:24"ExternalForce" -> (Quantity[-0.5 Normalize[ QuantityMagnitude[#["Velocity"]]](*An extra damping*), "Newtons"] &)? – Alex Trounev Feb 25 '22 at 05:07