How to determine the plane on which a surface lies?

Question

Is it possible with Mathematica to find an expression of the plane on which a surface lies ?

For instance, if we have a surface : $$f(x,y)=(1 - x - y) \log(1 - x - y) + 0.1 x \log(x) + 0.1 y \log(y) - x^2 - y^2 $$ is it possible to determine the plane $$S(x,y)=A+Bx+Cy $$ that is tangent to $f(x,y)$ or at least to make Mathematica plot it ?

Answer 1

You get the directions of the tangent plane at point {x,y} by: {1,0,D[f[x,y],x]} and {0,1,D[f[y,x],y]}.

Note: for numerical calculations you must take care not to call D[f[x,y],x] with numerical values for x.

Here is an example:

f[x_, y_] = (1 - x - y) Log[1 - x - y] + 0.1 x Log[x] + 0.1 y Log[y] -
    x^2 - y^2;
    Manipulate[Show[
      Plot3D[f[u, v], {u, 0, 1}, {v, 0, 1}, PlotLabel -> {x, y, 1 - x}, 
       PlotRange -> All],
      Graphics3D[{PointSize[0.02], Point[{x, y, f[x, y]}], Opacity[0.5], 
        InfinitePlane[{x, y, 
          f[x, y]}, {{1, 0, D[f[u, v], u]}, {0, 1, D[f[u, v], v]}} /. {u ->x, v -> y}]}]
      ]
     , {{x, 0.5}, 0.01, 1}, {{y, 0.4}, 0.01, 0.99 - x}
]

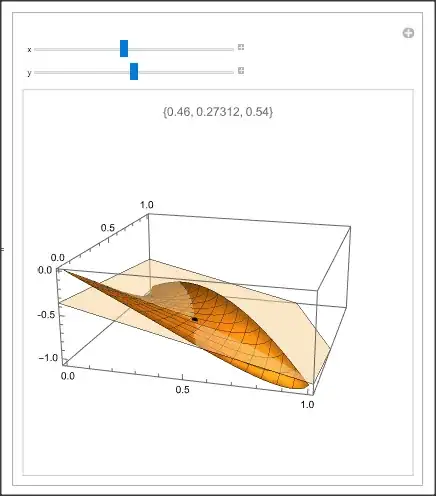
Note: the surface is not defined for all x and y values.