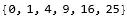This is how I would do it using Fourier method
\begin{align}
u_{t} & =u_{xx}\tag{1}\\
u_{x}\left( 0,t\right) & =0\nonumber\\
u_{x}\left( \pi,t\right) & =0\nonumber\\
u\left( x,0\right) & =\cos x-3\cos\left( 2x\right) +5\cos\left(
4x\right) \nonumber
\end{align}
Using Fourier method, the eigenvalues and eigefunctions for $y^{\prime\prime
}+\lambda y=0$ with B.C. $y^{\prime}\left( 0\right) =0,y^{\prime}\left(
\pi\right) =0$ are known to be
op = {-y''[x] + NeumannValue[0, True]}
eig = DEigenvalues[op, y[x], {x, 0, Pi}, 6]
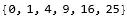
eigf = Last@DEigensystem[op, y[x], {x, 0, Pi}, 6]

Hence
\begin{align*}
\Phi_{n}\left( x\right) & =\cos\left( \sqrt{\lambda_{n}}x\right) \\
\lambda_{n} & =\left( \frac{n\pi}{L}\right) ^{2}
\end{align*}
Or for $L=\pi$
\begin{align*}
\Phi_{n}\left( x\right) & =\cos\left( nx\right) \\
\lambda_{n} & =n^{2}%
\end{align*}
Therefore the solution to the PDE is the Fourier series
\begin{equation}
u\left( x,t\right) =\sum_{n=1}^{\infty}b_{n}\left( t\right) \Phi
_{n}\left( x\right) \tag{2}
\end{equation}
And now the goal is to find $b_{n}\left( t\right) $ to finish the solution.
Substituting (2) in (1) gives
$$
\sum_{n=1}^{\infty}b_{n}^{\prime}\left( t\right) \Phi_{n}\left( x\right)
=\sum_{n=1}^{\infty}b_{n}\left( t\right) \Phi_{n}^{\prime\prime}\left(
x\right)
$$
But $\Phi_{n}^{\prime\prime}\left( x\right) =-\lambda_{n}\Phi_{n}\left(
x\right) $ since $\Phi_{n}\left( x\right) $ is eigenfunction. The above becomes
\begin{align*}
\sum_{n=1}^{\infty}b_{n}^{\prime}\left( t\right) \Phi_{n}\left( x\right)
& =-\sum_{n=1}^{\infty}\lambda_{n}b_{n}\left( t\right) \Phi_{n}\left(
x\right) \\
b_{n}^{\prime}\left( t\right) \Phi_{n}\left( x\right) +\lambda_{n}%
b_{n}\left( t\right) \Phi_{n}\left( x\right) & =0\\
b_{n}^{\prime}\left( t\right) +\lambda_{n}b_{n}\left( t\right) & =0\\
b_{n}^{\prime}\left( t\right) +n^{2}b_{n}\left( t\right) & =0
\end{align*}
This is first oder ode in $b_{n}\left( t\right) \,$. Solving gives
$$
b_{n}\left( t\right) =C_{n}e^{-n^{2}t}
$$
Substituting the above in (2) gives
\begin{equation}
u\left( x,t\right) =\sum_{n=1}^{\infty}C_{n}e^{-n^{2}t}\Phi_{n}\left(
x\right) \tag{3}
\end{equation}
Now $C_{n}$ are found from initial conditions. At $t=0$ the above becomes
\begin{equation}
\cos x-3\cos\left( 2x\right) +5\cos\left( 4x\right) =\sum_{n=1}^{\infty
}C_{n}\Phi_{n}\left( x\right) \tag{4}
\end{equation}
For $n=1$
\begin{align*}
\cos x & =C_{1}\Phi_{1}\left( x\right) \\
C_{1} & =\frac{\cos x}{\Phi_{1}\left( x\right) }=\frac{\cos x}{\cos\left(
x\right) }=1
\end{align*}
For $n=2$
\begin{align*}
-3\cos\left( 2x\right) & =C_{2}\Phi_{2}\left( x\right) \\
C_{2} & =\frac{-3\cos\left( 2x\right) }{\Phi_{2}\left( x\right) }
=\frac{-3\cos\left( 2x\right) }{\cos\left( 2x\right) }=-3
\end{align*}
For $n=4$
\begin{align*}
5\cos\left( 4x\right) & =C_{4}\Phi_{4}\left( x\right) \\
C_{4} & =5\frac{\cos\left( 4x\right) }{\Phi_{4}\left( x\right) }
=5\frac{\cos\left( 4x\right) }{\cos\left( 4x\right) }=5
\end{align*}
Substituting the above in (3) gives
\begin{align*}
u\left( x,t\right) & =C_{1}e^{-t}\Phi_{1}\left( x\right) +C_{2}%
e^{-4t}\Phi_{2}\left( x\right) +C_{4}e^{-16t}\Phi_{4}\left( x\right) \\
& =e^{-t}\cos\left( x\right) -3e^{-4t}\cos\left( 2x\right) +5e^{-16t}
\cos\left( 4x\right)
\end{align*}
Verify using Mathematica
ClearAll[u, x, t]
pde = D[u[x, t], t] == D[u[x, t], {x, 2}]
bc = {(D[u[x, t], x] == 0) /. x -> 0, (D[u[x, t], x] == 0) /. x -> Pi}
ic = u[x, 0] == Cos[x] - 3*Cos[2*x] + 5*Cos[4*x]
DSolve[{pde, bc, ic}, u[x, t], {x, t}]

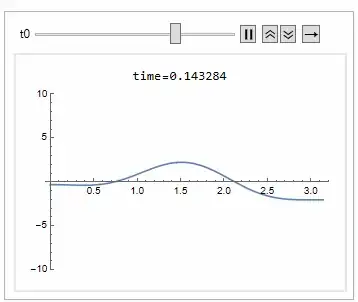
animation
Animate[Grid[{{Row[{"time=", t0}]}, {Plot[sol /. t -> t0, {x, 0, Pi},
PlotRange -> {Automatic, {-10, 10}}, ImageSize -> 300]}}], {t0,
0, .2}]