Simple Decision Tree for Tuples

Question

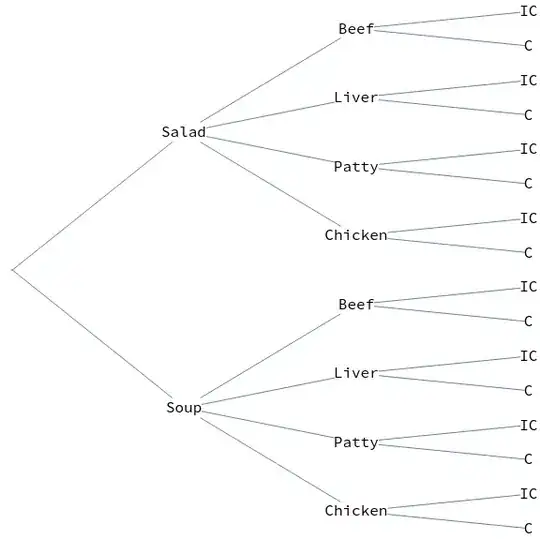
I would like to create a simple decision tree for a 3-course meal that looks something like the following:

The tuples can be created using the code:

Tuples[{{""}, {"Soup", "Salad"}, {"Chicken", "Patty", "Liver", 
   "Beef"}, {"C", "IC"}}]

to get

{{"", "Soup", "Chicken", "C"}, {"", "Soup", "Chicken", "IC"}, {"", 
  "Soup", "Patty", "C"}, {"", "Soup", "Patty", "IC"}, {"", "Soup", 
  "Liver", "C"}, {"", "Soup", "Liver", "IC"}, {"", "Soup", "Beef", 
  "C"}, {"", "Soup", "Beef", "IC"}, {"", "Salad", "Chicken", 
  "C"}, {"", "Salad", "Chicken", "IC"}, {"", "Salad", "Patty", 
  "C"}, {"", "Salad", "Patty", "IC"}, {"", "Salad", "Liver", 
  "C"}, {"", "Salad", "Liver", "IC"}, {"", "Salad", "Beef", "C"}, {"",
   "Salad", "Beef", "IC"}}

To get the decision tree, I've tried using the TreeGraph[] function, but it's too time-consuming writing out each paired rule and then I run into issues of repeats which I can't sort out. In any case, I would like to use the results from the code above, to generate a simple decisions tree. Any ideas?

kglr · Accepted Answer · 2022-03-14T05:58:45.447

layers = { {""}, {"Soup", "Salad"}, {"Chicken", "Patty", "Liver", "Beef"}, {"C", "IC"}};

eg = ExpressionGraph[ConstantArray[1, Rest[Length /@ layers]],  
      PerformanceGoal -> "Quality", 
      VertexStyle -> Black, 
      ImageSize -> Large, 
      AspectRatio -> 1, 
      GraphLayout -> {"LayeredEmbedding", "Orientation" -> Left}]

Almost there ... except the labeling of vertices. To this end, we (1) use BreadthFirstScan to get a list of rules (vLabeling) to make the vertices in each layer indexed consecutively, (2) make appropriate number of copies of the elements of layers to get a list of labels (vlabels).

vLabeling = Thread[First @ Last @ Reap @ 
      BreadthFirstScan[#, 1, {"PrevisitVertex" -> Sow}] -> VertexList[#]] &;
vlabels = Join @@ MapThread[PadRight[##, "Periodic"]&, 
    {layers, FoldList[Times, Length /@ layers]}];
SetProperty[eg, 
  {VertexShapeFunction -> (Text[Style[vlabels[[#2 /. vLabeling[eg]]], 16], #] &)}]

score 5 · Answer 2 · answered Mar 14 '22 at 00:10

It sounds like you're interested in the visualization (i.e. TreeGraph), so what follows targets that. If you're actually interested in a data structure that could be used to implement a decision tree, then there is a better approach.

Here's your data (I've replaced the empty string with "root" to keep things a bit clearer).

nodes = {{"root"}, {"Soup", "Salad"}, {"Chicken", "Patty", "Liver", "Beef"}, {"C", "IC"}}

We will attempt a graph, but it won't be a tree because nodes can have mutiple predecessors. We'll attempt a tree later.

edges = Flatten@Map[Apply[DirectedEdge], Tuples /@ Partition[nodes, 2, 1], {-2}];
Graph[edges, VertexLabels -> "Name"]

In order to get a tree, we'll need to give the nodes unique names. We can do this by first getting all of the paths/decisions and then prepending ancestor node names to each node (this is like a trie).

paths = Tuples[nodes];
treePaths = FoldList[StringJoin, #] & /@ paths;
treeEdges = 
  Union@Flatten@Map[Apply[DirectedEdge], Partition[#, 2, 1] & /@ treePaths, {-2}];
(At this point we have unique edges of the correct form for a tree, so we can use TreeGraph...)
TreeGraph[treeEdges, VertexLabels -> "Name"]
(You'll probably need to do some adjustments so that it looks nice, like setting the size or other display attributes.)

Wow! Thank you. This helps quite a bit. I still run into the issue of unique names. I would like to keep the non unique names but can’t figure out how to do this using TreeGraph — B flat, Mar 14 '22 at 01:35
Maybe you can use special characters or invisible characters to preserve uniqueness. I don't think TreeGraph will work otherwise, because you will end up with cycles/diamonds, and TreeGraph explicitly disallows that. — lericr, Mar 14 '22 at 03:45

Simple Decision Tree for Tuples

2 Answers2