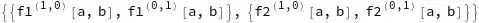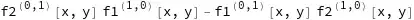5

I have a vector function $ f(x,y) = (f_1(x,y), f_2(x,y) ).$ I need to find the Jacobian matrix for $f$ evaluated at the point $(x,y) = (a,b).$

I learnt that I can use something like the following on Mathematica to find the Jacobian matrix:

Jacobian matrix $(f_1(x,y), f_2(x,y) )$ w.r.t. $x$, and $y.$

I need to evaluate the Jacobina matrix at the point $(x,y) = (a,b)$ using Mathematica.

How to do that?

Zizo
  • 153
  • 5

3 Answers3

6

Let f be a vector function:

f[x_, y_] := {f1[x, y], f2[x, y]};

Then the Jacobian is the matrix valued function:

D[f[x, y], {{x, y}}]

enter image description here

and the Jacobian at point {a,b} is:

D[f[x, y], {{x, y}}] /. {x->a,y->b}

enter image description here

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
5

You can do it as follows:

Vector field:

F[{x_, y_}] := Evaluate[{f1[x, y], f2[x, y]}]
X = {x, y};
X0 = {a, b};

The Jacobian Matrix:

J[{x_, y_}] = Simplify[D[F[X], {X}]];
MatrixForm@J[X]

enter image description here

The Jacobian at point $X_{0}=\left(a, b \right)$ is:

MatrixForm@J[X0]

enter image description here

E. Chan-López
  • 23,117
  • 3
  • 21
  • 44
4

If you have a look at this link you can take the code as appears there. Namely,

JacobianMatrix[f_List?VectorQ, x_List] := 
 Outer[D, f, x] /; Equal @@ (Dimensions /@ {f, x})

JacobianDeterminant[f_List?VectorQ, x_List] := 
 Det[JacobianMatrix[f, x]] /; Equal @@ (Dimensions /@ {f, x})

The Jacobian matrix is

JacobianMatrix[{f1[x, y], f2[x, y]}, {x, y}]

jac1

and you can evaluate at a point using either of the following:

JacobianMatrix[{f1[x, y], f2[x, y]}, {x, y}] /. {x :> a, y :> b}

With[{x = a, y = b}, JacobianMatrix[{f1[x, y], f2[x, y]}, {x, y}]]

both return the same result of course

jac2

Finally, the command for the Jacobian determinant is very similar

JacobianDeterminant[{f1[x, y], f2[x, y]}, {x, y}]

jac3

bmf
  • 15,157
  • 2
  • 26
  • 63