4

How can I get the numeric points {x,y} where the lines below intersect, please?

cvf = {{0.`, 
    0.`}, {-2.5866650924004158`, -1.2251749213103618`}, \
{2.5866650924004153`, 1.2251749213103618`}, {-0.46459988053166823`, 
    3.255060440892003`}, {0.46459988053166823`, -3.255060440892003`}, \
{3.0512649729320835`, -2.0298855195816414`}, {-3.051264972932084`, 
    2.0298855195816414`}};
prePLin[col_, pnt_] := {col, Dashed, 
  Line[{cvf[[pnt]]/2 + RotationMatrix[-90 Degree] . cvf[[pnt]]/2, 
    cvf[[pnt]]/2 + RotationMatrix[90 Degree] . cvf[[pnt]]/2}], 
  Line[{cvf[[pnt + 1]]/2 + 
     RotationMatrix[-90 Degree] . cvf[[pnt + 1]]/2, 
    cvf[[pnt + 1]]/2 + RotationMatrix[90 Degree] . cvf[[pnt + 1]]/2}]}
Graphics[{prePLin[Green, 2], prePLin[Blue, 4], prePLin[Red, 6]}]

enter image description here

I tried this answer

LineIntersectionPoint[{a_, b_}, {c_, d_}] := 
  (Det[{a, b}] (c - d) - Det[{c, d}] (a - b))/Det[{a - b, c - d}]

Tlins[pnt_] := {cvf[[pnt]]/2 + 
   RotationMatrix[-90 Degree] . cvf[[pnt]]/2, 
  cvf[[pnt]]/2 + RotationMatrix[90 Degree] . cvf[[pnt]]/2}
p1 = Table[Tlins[j], {j, {2, 3, 4}}];
p2 = Table[Tlins[j], {j, {5, 6, 7}}];


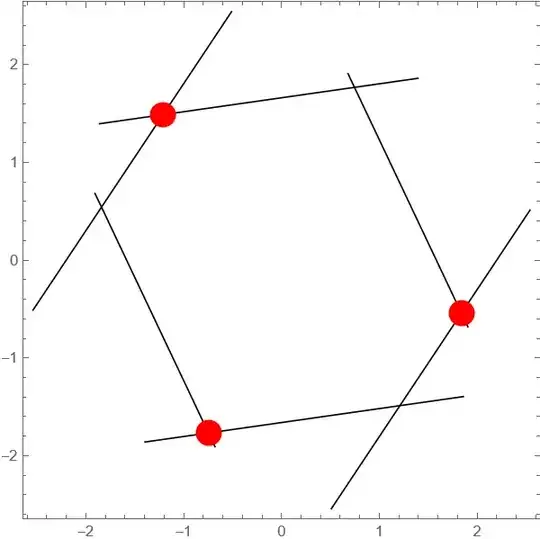
Graphics[{Line /@ {p1, p2}, Red, PointSize@.05, 
  Point /@ MapThread[LineIntersectionPoint, {p1, p2}]}, Frame -> True]

enter image description here

but it escapes three points?

MMA13
  • 4,664
  • 3
  • 15
  • 21
  • 3
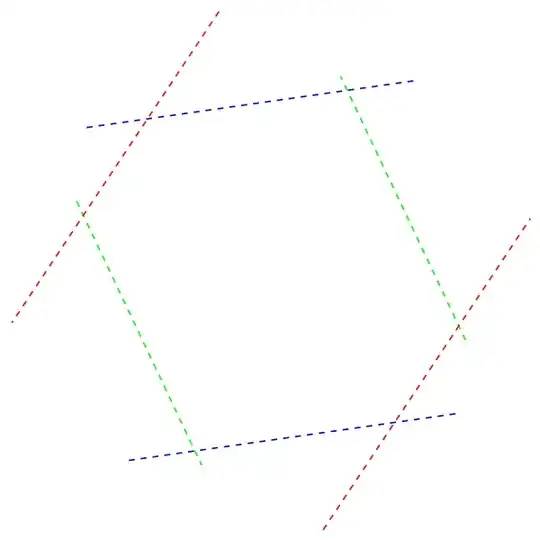
    try intersections = Graphics`Mesh`FindIntersections@ Graphics[{prePLin[Green, 2], prePLin[Blue, 4], prePLin[Red, 6]}]? – kglr Mar 24 '22 at 09:08

1 Answers1

4
    lines = Cases[{prePLin[Green, 2], prePLin[Blue, 4], prePLin[Red, 6]}, 
      Line[__], Infinity]

Briefly, tuples are created for all extracted lines. This will also have pairs with the same lines that are deleted. After the RegionIntersection command is applied there will be EmptyRegions found where lines don't intersect that have to be deleted. Then the duplicated points are removed.

ptsI = RegionIntersection @@@ (Tuples[lines, {2}] // 
      DeleteCases[#, {a_, a_}] &) /. EmptyRegion[_] :> Nothing // 
  DeleteDuplicates

{Point[{{-0.746437, -1.76723}}], Point[{{-1.84023, 0.542052}}], 
 Point[{{0.746437, 1.76723}}], Point[{{1.84023, -0.542052}}], 
 Point[{{-1.21104, 1.48783}}], Point[{{1.21104, -1.48783}}]}

Graphics[{{prePLin[Green, 2], prePLin[Blue, 4], prePLin[Red, 6]},
  AbsolutePointSize[6], Red, ptsI}]

enter image description here

EDIT

Following @bmf 's comment:

Let's say we have lines defined as above.

{Length@lines, Tuples[lines, {2}] // Length}

{6, 36}

Instead of comparing intersections with 36 pairs of lines, we would like to make tuples in a lower triangularized fashion between the lines. Extracting locations of lines to put into tuples:

t = Table[{i, j}, {i, 2, Length@lines}, {j, 1, i - 1}] // 
  Flatten[#, 1] &

{{2, 1}, {3, 1}, {3, 2}, {4, 1}, {4, 2}, {4, 3}, {5, 1}, {5, 2}, {5, 
  3}, {5, 4}, {6, 1}, {6, 2}, {6, 3}, {6, 4}, {6, 5}}

lineTuples = lines[[#]] & /@ t ;

Now there will be no need of deleting duplicates.

ptsI = RegionIntersection @@@ lineTuples /. EmptyRegion[_] :> Nothing

Length@lineTuples (* 15 *)
Syed
  • 52,495
  • 4
  • 30
  • 85
  • why does ptsI give 12 points? where only 6 are correct? – MMA13 Mar 24 '22 at 07:36
  • 1
    I have updated the answer. – Syed Mar 24 '22 at 07:36
  • @Syed this is wonderful. I just don't understand the need for DeleteDuplicates. I thought that DeleteCases would do the trick alone. – bmf Mar 24 '22 at 07:41
  • 1
    @bmf consider restoring your answer. It shows good usage of Mesh and I was gonna learn more from it. About your comment above, it starts with an embedded line graphic from where I extracted lines and made tuples. I can go a step further and Union the tuples with some effort after which there will be no need of deleting the duplicates. For large lists, it would be a judgement call as to whether to do it first or not, but it is something worth investigating. – Syed Mar 24 '22 at 07:55
  • 1
    @Syed not sure if you saw it or not, but it was not my answer. As I explained, I borrowed the code developed here. kglr has written a tremendous response, I just applied it. I don't think you'll have issues applying it in this example. Btw, I saw the addition you made to your answer, and many thanks for taking the time to do so. It has been a (+1) from me all along :-) – bmf Mar 24 '22 at 07:58
  • @Syed I can restore it, but I don't think it offers much. Yours is much better and the link provided is enough for the other approach I think – bmf Mar 24 '22 at 08:00