how can I arrange points to get the Circumference?

Question

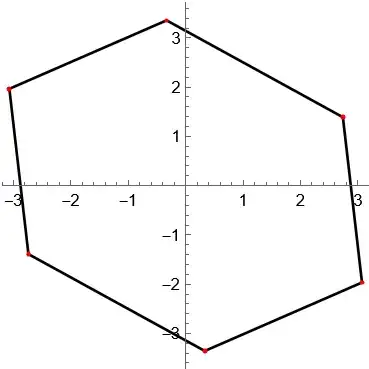
this is a simple example, points can circumvent complex shapes too.

BZponts {{-3.0725110665438153`, 
    1.9660166587475025`}, {-2.7397813916101534`, \
-1.389711956576523`}, {-0.3327296749336619`, 
    3.3557286153240256`}, {0.3327296749336619`, \
-3.3557286153240256`}, {2.739781391610154`, 
    1.389711956576523`}, {3.072511066543816`, -1.9660166587475025`}};
Show[Graphics[{FaceForm[None], EdgeForm[Black], Polygon[BZponts]}, 
  PlotRange -> {{-5, 5}, {-5, 5}}], 
 ListPlot[BZponts, PlotStyle -> Red]]

How can I sort the points to get a close shape like this

Does this question solve your problem ? https://mathematica.stackexchange.com/questions/58211/ordering-the-boundary-points-of-a-polygon — image_doctor, Mar 24 '22 at 10:49
I think the best way is use the original intersection lines in your previous question to build such cyclic polygon. Another language such PostScript implement the buildcyclie command,that is build a region from several curves. — cvgmt, Mar 24 '22 at 11:32
@cvgmt, but it is not always like that, I just used data from previous question as an example — MMA13, Mar 24 '22 at 11:59

cvgmt · Accepted Answer · 2022-03-25T07:46:35.767

Edit

Extract cyclic line from the convex polygon and list it points seems also work.

(Thanks @expression )

MeshPrimitives[ConvexHullMesh[BZponts], 2][[1, 1]]

{{-3.07251, 1.96602}, {-2.73978, -1.38971}, {0.33273, -3.35573}, {3.07251, -1.96602}, {2.73978, 1.38971}, {-0.33273, 3.35573}}

Original

bd = ConvexHullMesh[BZponts] // RegionBoundary;
pts = MeshCoordinates[bd];
lines = MeshCells[bd, "Multicells" -> True][[2]];
pts = pts[[lines[[1, 1, ;; , -1]]]];
{ListPlot[Append[#, First@#] &@pts, Joined -> True, AspectRatio -> 1],
   Graphics[{Red, Opacity[.2], AbsoluteThickness[10], bd}]} // Show

{2, 4, 6, 5, 3, 1}

how can I arrange points to get the Circumference?

1 Answers1